练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．观察如图所示的总阵图和相应的等式，探究其中的规律．

    ①1=12  ②1+3=22  ③1+3+5=32  ④1+3+5+7=42    ⑤1+3+5+7+9=52
    （1）在④和⑤后面的横线上分别写上相应的等式；
    （2）通过猜想写出第n个点阵图相应的等式．

    分析 （1）观察图形得到④中点的个数的和为1+3+5+7=16，则1+3+5+7=42；同样可得到⑤中的等式为1+3+5+7+9=52；
    （2）根据前面的等式的规律得到第n个点阵图中点的个数共有n2个，它有从1开始的n个连续奇数的和，于是得到1+3+5+7+…+（2n-1）=n2．

    解答 解：（1）④：1+3+5+7=42；⑤1+3+5+7+9=52；
    （2）1+3+5+7+…+（2n-1）=n2（n≥1的整数）．
    故答案为：1+3+5+7=42；1+3+5+7+9=52；

    点评 本题考查了规律型：图形的变化类：通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．按要求完成下列各题
    （1）化简：3a+（-8a+2）-3（3a-4）．
    （2）先化简，再求值：3（x2y-2xy）-2（x2y-3xy）-5x2y，其中x=-1，y=$\frac{1}{6}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：
    ①-4-28-（-19）+（-24）
    ②（-$\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$）÷（-$\frac{1}{36}$）
    ③（-3）3÷2$\frac{1}{4}$×（-$\frac{2}{3}$）2+4-23×（-$\frac{1}{3}$）
    ④-42-[-2-（5-0.5×$\frac{1}{3}$）×（-6）]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．当x=5时，式子ax3-bx+1的值是2，当x=-5时，求式子ax3-bx+2016的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在平行四边形ABCD中，AC，BD相交于点O，点E，F在AC上，且OE=OF，求证：BE=DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．计算
    （1）（1+$\frac{1}{{a}^{2}-1}$）÷$\frac{a}{a-1}$
    （2）$\frac{2a+2}{a-1}$÷（a+1）-$\frac{{a}^{2}-1}{{a}^{2}-2a+1}$
    （3）（$\frac{2}{3}$）2÷（$\frac{2}{3}$）2-（-2）-1÷（$\frac{1}{2}$）2-（$\frac{4}{5}$-0.2）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．先化简，再求值：（2a-b）2-4（a+2b）（a-2b），其中a=2，b=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．化简：
    （1）（x+y）（x-2y）-（x-2y）2
    （2）（$\frac{{x}^{2}}{x+2}$-x+2）÷$\frac{{x}^{3}-{2x}^{2}}{4{-x}^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

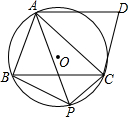    1．已知：如图，在平行四边形ABCD中，⊙O是经过A、B、C三点的圆，CD与⊙O相切于点C，点P是$\widehat{BC}$上的一个动点（点P不与B、C点重合），连接PA、PB、PC．
    （1）求证：CA=CB；
    （2）①点P满足当AC=AP时，△CPA≌△ABC，请说明理由；
    ②当∠ABC的度数为60时，四边形ABCD是菱形．

    查看答案和解析>>

    同步练习册答案