
 1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m.
1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m.科目:初中数学 来源: 题型:
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
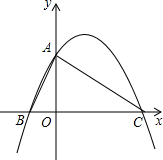 如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.
如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
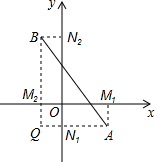 阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,
阅读材料:在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1-x2|,如果A(x1,y1),B(x2,y2)是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离.如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1-x2|,BQ=|y1-y2|,| (x1-x2)2+(y1-y2)2 |
| x2+(y-2)2 |
| (x-3)2+(y-1)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
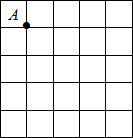 如图的正方形网格中,每个小正方形边长均为1,点A固定在格点(即小正方形的顶点)上,请按步骤要求作图并解答:
如图的正方形网格中,每个小正方形边长均为1,点A固定在格点(即小正方形的顶点)上,请按步骤要求作图并解答:| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com