
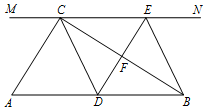
 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上分析 (1)证出AC∥DE,得出四边形ADEC是平行四边形,即可得出结论;
(2)①先证出BD=CE,得出四边形BECD是平行四边形,再由直角三角形斜边上的中线性质得出CD=$\frac{1}{2}$AB=BD,即可得出四边形BECD是菱形;
②当∠A=45°时,△ABC是等腰直角三角形,由等腰三角形的性质得出CD⊥AB,即可得出四边形BECD是正方形.
解答  (1)证明:∵DE⊥BC,
(1)证明:∵DE⊥BC,
∴∠DFB=90°.
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE.
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)①证明:∵D为AB中点,
∴AD=BD.
∵CE=AD,
∴BD=CE.
∵BD∥CE,
∴四边形BECD是平行四边形.
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
②当∠A=45°时,四边形BECD是正方形.
理由如下:∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°,
∴AC=BC.
∵D为BA中点,
∴CD⊥AB,
∴∠CDB=90°.
∵四边形BECD是菱形,∠CDB=90°,
∴四边形BECD是正方形.
点评 本题考查了平行四边形的判定与性质、正方形的判定、菱形的判定、直角三角形斜边上的中线性质;熟练掌握平行四边形的判定与性质,并能进行推理论证是解决问题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:填空题
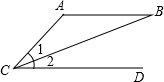 如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.
如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
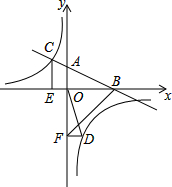 如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.
如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)的图象在第二象限交于点C,CE⊥x轴,垂足为点E,sin∠ABO=$\frac{\sqrt{5}}{5}$,OB=2,OE=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
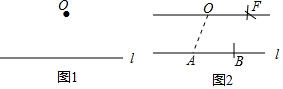 下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
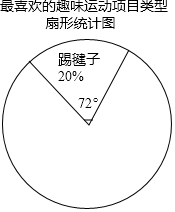 某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.| 项目类型 | 频数 | 频率 |
| 跳长绳 | 25 | a |
| 踢毽子 | 20 | 0.2 |
| 背夹球 | b | 0.4 |
| 拔河 | 15 | 0.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
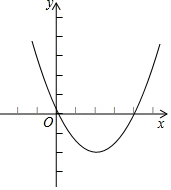 在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).
在平面直角坐标系xOy中,直线y=ax+b与抛物线y=ax2+bx交于A、B两点(点A在点B的左侧),点C的坐标为(a,b).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com