
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=﹣5x2+20x,请根据要求解答下列问题:
(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是多少?
(2)在飞行过程中,小球从飞出到落地所用时间是多少?
(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少?

【答案】(1)在飞行过程中,当小球的飞行高度为15m时,飞行时间是1s或3s;(2)在飞行过程中,小球从飞出到落地所用时间是4s;(3)在飞行过程中,小球飞行高度第2s时最大,最大高度是20m.
【解析】
(1)根据题目中的函数解析式,令y=15即可解答本题;
(2)令y=0,代入题目中的函数解析式即可解答本题;
(3)将题目中的函数解析式化为顶点式即可解答本题.
(1)当y=15时,
15=﹣5x2+20x,
解得,x1=1,x2=3,
答:在飞行过程中,当小球的飞行高度为15m时,飞行时间是1s或3s;
(2)当y=0时,
0═﹣5x2+20x,
解得,x3=0,x2=4,
∵4﹣0=4,
∴在飞行过程中,小球从飞出到落地所用时间是4s;
(3)y=﹣5x2+20x=﹣5(x﹣2)2+20,
∴当x=2时,y取得最大值,此时,y=20,
答:在飞行过程中,小球飞行高度第2s时最大,最大高度是20m.


科目:初中数学 来源: 题型:
【题目】近年来,地震、泥石流等自然灾害频繁发生,造成极大的生命和财产损失.为了更好地做好“防震减灾”工作,我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查,调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级.小明根据调查结果绘制了如图1、2的统计图,请根据提供的信息回答问题:
(1)本次调查中,样本容量是________;
(2)扇形统计图中“基本了解”部分所对应的扇形圆心角是________;在该校2000名学生中随机提问一名学生,对“防震减灾”不了解的概率的估计值为________;
(3)请在图2中补全频数分布直方图.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进货价每个10元的商品按售价18元售出时,每天可卖出60个.商店经理到市场上做了一番调查后发现,若将这种商品的售价每提高1元,则日销售量就减少5个;若将这种商品的售价每降低1元,则日销售量就增加10个。为获得每日最大利润,此商品售价应定为每个多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
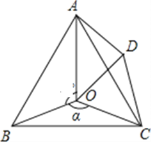
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=130°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上的一动点,连接AC并延长交⊙O于D,过点D作直线交OB延长线于E,且DE=CE,已知OA=8.
(1)求证:ED是⊙O的切线;
(2)当∠A=30°时,求CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,﹣3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
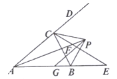
【题目】如图所示,在![]() 中,内角
中,内角![]() 与外角
与外角![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() ,
,![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() 、
、![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() 垂直平分
垂直平分![]() ;④
;④![]() .其中正确的是( )
.其中正确的是( )
A. ①②④B. ①③④C. ②③④D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
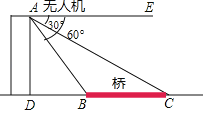
【题目】小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度AD,小亮通过操控器指令无人机测得桥头B,C的俯角分别为∠EAB=60°,∠EAC=30°,且D,B,C在同一水平线上.已知桥BC=30米,求无人机飞行的高度AD.(精确到0.01米.参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com