【题目】如图，OA，OB是⊙O的两条半径，OA⊥OB，C是半径OB上的一动点，连接AC并延长交⊙O于D，过点D作直线交OB延长线于E，且DE=CE，已知OA=8．
（1）求证：ED是⊙O的切线；
（2）当∠A=30°时，求CD的长．
【答案】（1）证明见解析；（2）
.
【解析】
（1）如图连接OD．欲证明DE是切线，只要证明OD⊥DE即可；
（2）解直角三角形求出OC，只要证明CD=OC即可解决问题；
（1）证明：如图连接OD．
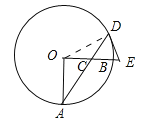
∵OA=OD，∴∠A=∠ODA．
∵OA⊥OB，∴∠AOB=90°，∴∠A+∠ACO=90°．
∵ED=EB，∴∠EDB=∠EBD=∠ACO，∴∠ODA+∠EDC=90°，∴OD⊥DE，∴DE是⊙O的切线．
（2）在Rt△AOC中，∵OA=8，∠A=30°，∴OC=OAtan30°=．
∵OA=OD，∴∠ODA=∠A=30°，∠DOA=120°，∠DOC=30°，∴∠DOC=∠ODC=30°，∴CD=OC=．
科目：初中数学 来源： 题型：
【题目】（12分）某工厂生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本
（万元/吨）与产量
（吨）之间是一次函数关系，函数
与自变量的部分对应值如下表：
| 10 | 20 | 30 |
| 45 | 40 | 35 |
（1）求
与
的函数关系式，并写出自变量的取值范围；
（2）当投入生产这种产品的总成本为1200万元时，求该产品的总产量；（注：总成本=每吨成本×总产量）
（3）市场调查发现，这种产品每月销售量
（吨）与销售单价
（万元/吨）之间满足如图所示的函数关系．该厂第一个月按同一销售单价卖出这种产品25吨，请求出该厂第一个月销售这种产品获得的利润．（注：利润=售价—成本）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，∠BAC=540，以AB为直径的⊙O分别交AC，BC于点D，E，过点B作⊙O的切线，交AC的延长线于点F。
（1）求证：BE=CE；
（2）求∠CBF的度数；
（3）若AB=6，求
的长。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点M（n，﹣n ）在第二象限，过点M的直线y=kx+b（0＜k＜1）分别交x轴、y轴于点A，B，过点M作MN⊥x轴于点N，则下列点在线段AN的是（ ）
A. （（k﹣1）n，0） B. （（k+
）n，0）） C. （
，0） D. （（k+1）n，0）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一小球沿与地面成一定角度的方向飞出，小球的飞行路线是一条抛物线，如果不考虑空气阻力，小球的飞行高度y（单位：m）与飞行时间x（单位：s）之间具有函数关系y=﹣5x2+20x，请根据要求解答下列问题：
（1）在飞行过程中，当小球的飞行高度为15m时，飞行时间是多少？
（2）在飞行过程中，小球从飞出到落地所用时间是多少？
（3）在飞行过程中，小球飞行高度何时最大？最大高度是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在足够大的空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．
（1）若a=20，所围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；
（2）求矩形菜园ABCD面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为执行“两免一补”政策，某地区2014年投入教育经费2500万元，预计到2016年，三年共投入8275万元．设投入教育经费的年平均增长率为x，那么下列方程正确的是( )
A. 2500x2
8275 B. 2500(1+x%)28275
C. 2500(1+x)28275 D. 2500+2500(1+x)+2500(1+x)28275
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系，跨度AB=44米，∠A=45°，AC1=4米，点D2的坐标为(-13，-1.69)，则桥架的拱高OH=________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
