练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，2BD=3DC，E是AC的中点，如S△ABC=10，则S△ADE=( )

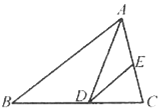
    A.5B.4 C.3 D.2

    【答案】D

    【解析】

    由已知可证得BD：DC=3:2，由此可推出S△ABD：S△ADC=3：2，再根据S△ABD+S△ADC= S△ABC=10 ，求出△ADC的面积，然后根据三角形的中线分得的两个三角形的面积相等，可求出△ADE的面积.

    解：∵2BD=3DC，

    ∴BD：DC=3：2，

    ∴S△ABD：S△ADC=3：2，

    设S△ABD=3x，S△ADC=2x，

    ∵S△ABD+S△ADC= S△ABC=10，

    ∴3x+2x=10，

    解得：x=2，

    ∴S△ADC=2×2=4，

    ∵点E是AC的中点，即DE是△ADC的中线，

    ∴S△ADC=2S△ADE=4，

    ∴S△ADE=2，

    故答案为：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，OA，OB是⊙O的两条半径，OA⊥OB，C是半径OB上的一动点，连接AC并延长交⊙O于D，过点D作直线交OB延长线于E，且DE=CE，已知OA=8．

    （1）求证：ED是⊙O的切线；

    （2）当∠A=30°时，求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，折叠长方形的边AD，点D落在BC边的点F处，AB＝8cm，BC＝10cm，求△ECF的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O的半径为5，EF是长为8的弦，OG⊥EF于点G，点A在GO的延长线上，且AO=13．弦EF从图1的位置开始绕点O逆时针旋转，在旋转过程中始终保持OG⊥EF，如图2．

    [发现]在旋转过程中，

    （1）AG的最小值是　 　，最大值是　 　．

    （2）当EF∥AO时，旋转角α=　 　．

    [探究]若EF绕点O逆时针旋转120°，如图3，求AG的长．

    [拓展]如图4，当AE切⊙O于点E，AG交EO于点C，GH⊥AE于H．

    （1）求AE的长．

    （2）此时EH=　 　，EC=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

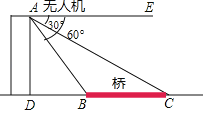
    【题目】小亮在某桥附近试飞无人机，如图，为了测量无人机飞行的高度AD，小亮通过操控器指令无人机测得桥头B，C的俯角分别为∠EAB=60°，∠EAC=30°，且D，B，C在同一水平线上．已知桥BC=30米，求无人机飞行的高度AD．（精确到0.01米．参考数据：≈1.414，≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知方程；则①当取什么值时，方程有两个不相等的实数根？②当取什么值时，方程有两个相等的实数根？③当取什么值时，方程没有实数根？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1， 在 中，，.点O是BC的中点，点D沿B→A→C方向从B运动到C.设点D经过的路径长为，图1中某条线段的长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是图1中的 ( )

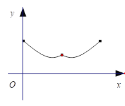
    图1 图2

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】开学初，为丰富教师们的业余生活，我校组织所有教师前往重庆大剧院观看演出。重庆大剧院的演出门票价格方案如下：1.票价根据座位区域不同定价不同，一区票价为120元/张，二区票价为100元/张；2.离退休教师各区均享受八折优惠。已知本次活动实到教师700人，若本次活动每人均购买二区票则需67200元。

    （1）求参加本次活动的在职教师、离退休教师分别有多少人；

    （2）为庆祝重阳节，重庆在大剧院调整了票价方案，将200张一区演出票票价每张降低了元，将全部二区演出票票价每张降低了元，离退休教师可在降价后仍享受八折优惠。若学校决定将200张一区演出票全部购入并优先发放给离退休教师和部分在职教师，其余教师均购买二区票，且校方希望总门票费用不超过66420元，求的最小值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系中，矩形OABC的顶点O、A、C的坐标分别为(0，0)、A(a，0)、C(0，b)，且a、b满足.

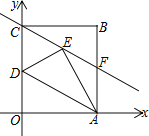
    (1)矩形的顶点B的坐标是______.

    (2)若D是OC中点，沿AD折叠矩形OABC使O点落在E处，折痕为DA，连CE并延长交AB于F，求直线CE的解析式；

    (3)将(2)中直线CE向左平移个单位交y轴于M，N为第二象限内的一个动点，且∠ONM＝135°，求FN的最大值.

    查看答案和解析>>

    同步练习册答案