Question

【题目】已知⊙O的半径为5，EF是长为8的弦，OG⊥EF于点G，点A在GO的延长线上，且AO=13．弦EF从图1的位置开始绕点O逆时针旋转，在旋转过程中始终保持OG⊥EF，如图2．

[发现]在旋转过程中，

（1）AG的最小值是　 　，最大值是　 　．

（2）当EF∥AO时，旋转角α=　 　．

[探究]若EF绕点O逆时针旋转120°，如图3，求AG的长．

[拓展]如图4，当AE切⊙O于点E，AG交EO于点C，GH⊥AE于H．

（1）求AE的长．

（2）此时EH=　 　，EC=　 　．

Answer 1

【答案】发现：（1）10，16；（2）90°或270°；探究：AG=；拓展：（1）AE=12；（2），．

【解析】

发现：（1）根据垂径定理得：在Rt△EOG中，根据勾股定理求出OG=3，由旋转知，点G的轨迹是以点O为圆心，OG=3为半径的圆，即可求出AG的最大值与最小值.

（2）根据OG⊥EF，EF∥OA，得出OG⊥OA，即可求出旋转角度.

探究：过点G作GQ⊥OA于Q，在Rt△OQG中，求出∠GOQ的度数，根据含角的直角三角形的性质求出即可求出AG的长

拓展：（1）根据切线的性质得到∠OEA=90°，根据勾股定理即可求出AE的长.

（2）过点G作GP⊥OE于P，易证四边形EHGP是矩形，证明△OGE∽△OPG，根据相似三角形的性质得到即可求出的长度，即可求出EH的长度，再根据△AEC∽△AHG，求出EC的长度.

发现：（1）如图1，

连接OE，

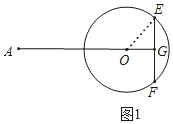
∵OG⊥EF，

∴

在Rt△EOG中，OE=5，根据勾股定理得，OG=3，

由旋转知，点G的轨迹是以点O为圆心，OG=3为半径的圆，

∴AG最大=OA+OG=13+3=16，

AG最小=OA﹣OG=13﹣3=10，

故答案为：10，16；

（2）∵OG⊥EF，EF∥OA，

∴OG⊥OA，

∴旋转角α=90°或270°，

故答案为90°或270°；

探究：如图3，

过点G作GQ⊥OA于Q，

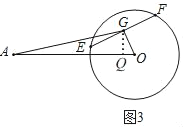
在Rt△OQG中，∠GOQ=180°﹣120°=60°，OG=3，

∴

∴

在Rt△AQG中，

拓展：（1）∵AE切⊙O于E，

∴∠OEA=90°，

在Rt△AEO中，

（2）如图4，

过点G作GP⊥OE于P，

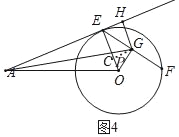
∵HG⊥AE，OE⊥AE，

∴四边形EHGP是矩形，

∴HG=EP，EH=PG，

∵∠OGE=∠OPG=90°，∠GOE=∠POG，

∴△OGE∽△OPG，

∴

∴

∴

∴

∵OE⊥AE，HG⊥AE，

∴CE∥HG，

∴△AEC∽△AHG，

∴

∴

∴

故答案为：