
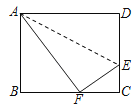
【题目】如图,折叠长方形的边AD,点D落在BC边的点F处,AB=8cm,BC=10cm,求△ECF的周长.
【答案】12cm
【解析】
根据矩形的性质得DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则FC=4,设EC=x,则DE=EF=8﹣x,在Rt△EFC中,根据勾股定理得x2+42=(8﹣x)2,然后解方程即可求出x,再求△EFC的周长即可.
解:∵四边形ABCD为矩形,
∴DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,
∵折叠矩形的一边AD,使点D落在BC边的点F处
∴AF=AD=10,DE=EF,
在Rt△ABF中,BF=![]() ,
,
∴FC=BC﹣BF=4,
设EC=x,则DE=8﹣x,EF=8﹣x,
在Rt△EFC中,
∵EC2+FC2=EF2,
∴x2+42=(8﹣x)2,
解得x=3,
∴EC=3cm,EF=5cm,
∴△EFC的周长=EC+EF+FC=3+5+4=12cm.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=540,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F。

(1)求证:BE=CE;
(2)求∠CBF的度数;
(3)若AB=6,求![]() 的长。
的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为执行“两免一补”政策,某地区2014年投入教育经费2500万元,预计到2016年,三年共投入8275万元.设投入教育经费的年平均增长率为x,那么下列方程正确的是( )
A. 2500x2![]() 8275 B. 2500(1+x%)2
8275 B. 2500(1+x%)2![]() 8275
8275
C. 2500(1+x)2![]() 8275 D. 2500+2500(1+x)+2500(1+x)2
8275 D. 2500+2500(1+x)+2500(1+x)2![]() 8275
8275
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣![]() x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
x2+bx+c的图象经过A(2,0),B(0,﹣6)两点,
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠BAC, 点E正好在BD的垂直平分线上,且AB=6,则△DBE的周长是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD在直角坐标系中的位置如图所示,其中边AD和边BC都与x轴平行,边AB和边CD都与y轴平行,且D(2,3),点C的纵坐标是-1,反比例函数y=![]() (k≠0)的图像过点C,与边AB交于点E.
(k≠0)的图像过点C,与边AB交于点E.

(1)求直线OD的表达式和此反比例函数的解析式:
(2)如果点B到y轴的距离是4,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com