
 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 单项式和多项式统称整式 | |
| B. | 有公共端点的两条射线组成的图形叫做角 | |
| C. | 两点之间的所有连线中,线段最短 | |
| D. | 由几个方程组成的一组方程叫做方程组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 方差 | |
| (1)班 | 89 | 100 | 96 | 118 | 97 | 94 |
| (2)班 | 100 | 95 | 110 | 91 | 104 | 44.4 |
| 优秀率 | 中位数 | |
| (1)班 | 40% | 97 |
| (2)班 | 60% | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
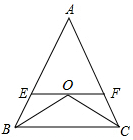 如图,在△ABC中∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB.若过点O作直线EF和边BC平行,与AB交于点E,与AC交于点F,则线段EF和EB,FC之间有怎样的数量关系并证明?
如图,在△ABC中∠ABC=∠ACB,BO平分∠ABC,CO平分∠ACB.若过点O作直线EF和边BC平行,与AB交于点E,与AC交于点F,则线段EF和EB,FC之间有怎样的数量关系并证明?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
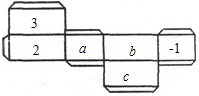 如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
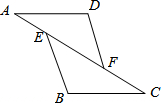 如图,已知,在△ADF和△CBE中,A、E、F、C在同一直线上,AE=CF,AD∥BC,那么添加一个条件后,使得△ADF≌△CBE,所用的判定方法是SAS.
如图,已知,在△ADF和△CBE中,A、E、F、C在同一直线上,AE=CF,AD∥BC,那么添加一个条件后,使得△ADF≌△CBE,所用的判定方法是SAS.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com