
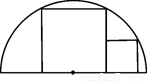
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.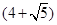 cm B.9 cm
C.
cm B.9 cm
C. cm D.
cm D. 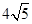 cm
cm
D
【解析】
试题分析:

连接OA、OB、OE,
∵四边形ABCD是正方形,
∴AD=BC,∠ADO=∠BCO=90°,
∵在Rt△ADO和Rt△BCO中
∵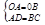 ,
,
∴Rt△ADO≌Rt△BCO,
∴OD=OC,
∵四边形ABCD是正方形,
∴AD=DC,
设AD=acm,则OD=OC= DC=
DC= AD=
AD= acm,
acm,
在△AOD中,由勾股定理得:OA=OB=OE=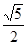 acm,
acm,
∵小正方形EFCG的面积为16cm2,
∴EF=FC=4cm,
在△OFE中,由勾股定理得: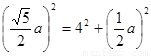 ,
,
解得:a=-4(舍去),a=8,
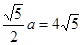 (cm),
(cm),
故选D.
考点:垂径定理;勾股定理.
点评:本题考查了全等三角形的性质和判定,勾股定理的应用,主要考查学生运用定理进行计算的能力,用的数学思想是方程思想.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013届湖北宜城九年级上学期期中考试数学试卷(有解析) 题型:单选题
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )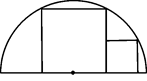
A.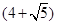 cm cm | B.9 cm | C.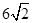 cm cm | D.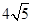 cm cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com