
【题目】如图,在![]() 中,
中,![]() ,DE是过点A的直线,
,DE是过点A的直线,![]() 于点D,
于点D,![]() 于点E,
于点E,![]() .
.
![]() 若BC在DE的同侧
若BC在DE的同侧![]() 如图
如图![]() 求证:
求证:![]() .
.
![]() 若BC在DE的两侧
若BC在DE的两侧![]() 如图
如图![]() ,其他条件不变,
,其他条件不变,![]() 中的结论还成立吗?
中的结论还成立吗?![]() 不需证明
不需证明![]()

【答案】(1)详见解析;(2)AB⊥AC.
【解析】
(1)根据直角三角形全等的判定方法HL易证得△ABD≌△CAE,可得∠DAB=∠ACE,再根据三角形内角和定理即可证得结论;(2)与(1)同理结论仍成立.
(1)证明:∵BD⊥DE于点D,CE⊥DE于点E,
∴△ABD和△CAE均为直角三角形.
在Rt△ABD和Rt△CAE中,![]() ,
,
∴Rt△ABD≌Rt△CAE(HL),
∴∠ABD=∠CAE.
又∵∠ABD+∠BAD=90°,
∴∠CAE+∠BAD=90°,
∴∠BAC=180°﹣(∠CAE+∠BAD)=90°,
∴AB⊥AC.
(2)解:AB⊥AC,理由如下:
同(1)可证出:Rt△ABD≌Rt△CAE(HL),
∴∠ABD=∠CAE.
又∵∠ABD+∠BAD=90°,
∴∠BAC=∠CAE+∠BAD=90°,
∴AB⊥AC.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】某校冬季会把课间操改为跑步,但是发现部分学生没有穿运动鞋的习惯,为保证学生的安全,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制出如下两幅不完整的统计图,请根据相关信息,解答下列问题.

(I)本次接受随机抽样调查的学生人数为_____;
(Ⅱ)在条形统计图中,请把空缺部分补充完整;
(Ⅲ)求本次调查获取的样本数据的众数与中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC; ②∠BCE+∠BCD=180°; ③AF2=EC2﹣EF2; ④BA+BC=2BF.其中正确的是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P,Q分别是边长为4 cm的等边三角形ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1 cm/s,连接AQ,CP,相交于点M.下面四个结论正确的有________(填序号).①BP=CM; ②△ABQ ≌△CAP ;③∠CMQ的度数不变,始终等于60;④当第![]() s或
s或![]() s时,△PBQ为直角三角形.
s时,△PBQ为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
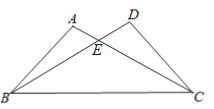
【题目】如图,已知∠A=∠D有下列五个条件①AE=DE ②BE=CE ③AB=DC ④∠ABC=∠DCB⑤AC=BD能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A、B、C在同一直线上,AB=2,BC=1,分别以AB、BC为边,在AC同侧作等边△ABD和等边△BCE,分别联结AE、CD.
(1)找出图中的全等三角形(不添加辅助线),并证明你的结论.

(2)线段AE与线段CD的关系是:AE CD(填>、=、<).AE与CD的夹角是: .
(3) △ABD固定不动,使△BCE绕着点B旋转,①这时(2)得出的结论还成立吗(不要求证明)?
②在旋转过程中,线段DC的长是变化的,它的变化范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com