
����Ŀ����֪����ͼ����A��B��C��ͬһֱ���ϣ�AB=2��BC=1���ֱ���AB��BCΪ�ߣ���ACͬ�����ȱ���ABD�͵ȱ���BCE���ֱ�����AE��CD.
��1���ҳ�ͼ�е�ȫ�������Σ������Ӹ����ߣ�����֤����Ľ���.

(2)�߶�AE���߶�CD�Ĺ�ϵ�ǣ�AE CD����>��=��<��.AE��CD�ļн��ǣ� .
(3) ��ABD�̶�������ʹ��BCE���ŵ�B��ת������ʱ��2���ó��Ľ��ۻ������𣨲�Ҫ��֤������
������ת�����У��߶�DC�ij��DZ仯�ģ����ı仯��Χ�� .
���𰸡���1������������2������������3��������.
��������
��1����������ɵ���ABE�ա�DBC��
��2������ABE�ա�DBC�ã�AE=CD, ��BAE=��BDC����BDC+��BCD=180��-60��-60��=60�����ʿɵ�AE��CD�ļн�Ϊ��BAE+��BCD=��BDC+��BCD=60�㣻
��3���ٳ�����
�ڵ�BC��DB��ʱ��DC��̵���1����BC��DB���ӳ�����ʱ��DC�����3���Ӷ��ɵý���.
��1��![]() ��
��
֤����![]() �ǵȱ������Σ�
�ǵȱ������Σ�
![]() ��
��
![]() �ǵȱ������Σ�
�ǵȱ������Σ�
![]()
![]()
��![]()
��![]() ��
��![]() ��
��
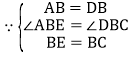
![]()
(2)�߶�AE���߶�CD�Ĺ�ϵ�ǣ�AE=CD��AE��CD�ļн��ǣ�![]() .
.
(3) �� ��2���ó��Ľ����Գ���.
�� ����ת�����У��߶�DC�ij��DZ仯�ģ����ı仯��Χ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ��DE�ǹ���A��ֱ�ߣ�
��DE�ǹ���A��ֱ�ߣ�![]() �ڵ�D��
�ڵ�D��![]() �ڵ�E��
�ڵ�E��![]() ��
��
![]() ��BC��DE��ͬ��
��BC��DE��ͬ��![]() ��ͼ
��ͼ![]() ��֤��
��֤��![]() ��
��
![]() ��BC��DE������
��BC��DE������![]() ��ͼ
��ͼ![]() �������������䣬
�������������䣬![]() �еĽ��ۻ�������
�еĽ��ۻ�������![]() ����֤��
����֤��![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC�͡�ABC��ƽ�����ཻ�ڵ�O������O��EF��AB��BC��F����AC��E������O��OD��BC��D�������ĸ����ۣ�
�١�AOB=90��+![]() ��C����AE+BF=EF���۵���C=90��ʱ��E��F�ֱ���AC��BC���е㣻����OD=a��CE+CF=2b����S��CEF=ab��������ȷ���ǣ�������
��C����AE+BF=EF���۵���C=90��ʱ��E��F�ֱ���AC��BC���е㣻����OD=a��CE+CF=2b����S��CEF=ab��������ȷ���ǣ�������

A. �٢� B. �ۢ� C. �٢ڢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AD=AE����B=��C����BAE=��CAD��BD��CE���ڵ�F��
��֤����1��AB=AC����2��FB=FC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ĵ���װ��һ��һ��2������Щ�����ɫ�ⶼ��ͬ��С�մӴ����������һ��������ɫ��Żش��У��ٴӴ����������һ�������ζ���������ĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڡ�ABC�У�BC=a��AC=b��AB=c������C=90�㣬��ͼ1������a2+b2=c2������ABCΪ���������ʱ��С�����룺a2+b2��c2 �� �������£���ͼ2������A��AD��CB�ڵ�D����CD=x����Rt��ADC�У�AD2=b2��x2 �� ��Rt��ADB�У�AD2=c2����a��x��2
��a2+b2=c2+2ax
��a��0��x��0
��2ax��0
��a2+b2��c2
�൱��ABCΪ���������ʱ��a2+b2��c2
����С���IJ�������ȷ�ģ�
��1��������룬����ABCΪ�۽�������ʱ��a2+b2��c2�Ĵ�С��ϵ��
��2����ܰ��ʾ����ͼ3�У���BC���ϵĸߣ�
��3��֤�������Ľ����Ƿ���ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ10���ף���E�ڱ�AB�ϣ���AE=4���ף������P���߶�BC����2����/����ٶ���B����C���˶���ͬʱ����Q���߶�CD����C����D���˶������˶�ʱ��Ϊt�룮
��1������Q���˶��ٶ����P���˶��ٶ���ȣ�����2�����BPE����CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ���tΪ��ֵʱ���ܹ�ʹ��BPE����CQPȫ�ȣ���ʱ��Q���˶��ٶ�Ϊ���٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ ![]() �У�
�У�![]() ���ף�
���ף�![]() ��
��![]() ���ף���
���ף��� ![]() Ϊ
Ϊ ![]() ���е㣮�����
���е㣮����� ![]() ���߶�
���߶� ![]() ����
���� ![]() ����/����ٶ���
����/����ٶ��� ![]() ����
���� ![]() ���˶���ͬʱ����
���˶���ͬʱ���� ![]() ���߶�
���߶� ![]() ����
���� ![]() ����
���� ![]() ����/����ٶ���
����/����ٶ��� ![]() ���˶������˶���ʱ��Ϊ
���˶������˶���ʱ��Ϊ ![]() �룮
�룮

��1��ֱ��д����
��BD��_______���ף� ��BP��________���ף�
��CP��_______���ף� ��CQ��_______���ף�
�����ú� ![]() ��a�Ĵ���ʽ��ʾ��
��a�Ĵ���ʽ��ʾ��
��2������ ![]() ��
��![]() ��
��![]() ������������
������������ ![]() ��
��![]() ��
��![]() Ϊ�����������ȫ�ȣ�����
Ϊ�����������ȫ�ȣ����� ![]() ��t��ֵ��
��t��ֵ��
��3������ ![]() �ԣ�
�ԣ�![]() ���е��˶��ٶȴӵ�
���е��˶��ٶȴӵ� ![]() ��������
�������� ![]() ��ԭ�����˶��ٶȴӵ�
��ԭ�����˶��ٶȴӵ� ![]() ͬʱ����������ʱ����
ͬʱ����������ʱ���� ![]() �����˶������˶���ʱ��Ϊ
�����˶������˶���ʱ��Ϊ ![]() �룻ֱ��д��t= ��ʱ��
�룻ֱ��д��t= ��ʱ�� ![]() ���
��� ![]() ��һ��������
��һ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com