
����Ŀ�����ڡ�ABC�У�BC=a��AC=b��AB=c������C=90�㣬��ͼ1������a2+b2=c2������ABCΪ���������ʱ��С�����룺a2+b2��c2 �� �������£���ͼ2������A��AD��CB�ڵ�D����CD=x����Rt��ADC�У�AD2=b2��x2 �� ��Rt��ADB�У�AD2=c2����a��x��2
��a2+b2=c2+2ax
��a��0��x��0
��2ax��0
��a2+b2��c2
�൱��ABCΪ���������ʱ��a2+b2��c2
����С���IJ�������ȷ�ģ�
��1��������룬����ABCΪ�۽�������ʱ��a2+b2��c2�Ĵ�С��ϵ��
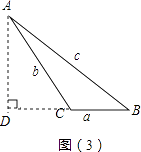
��2����ܰ��ʾ����ͼ3�У���BC���ϵĸߣ�
��3��֤�������Ľ����Ƿ���ȷ��
���𰸡�
��1��
�⣺����ABCΪ�۽�������ʱ��a2+b2��c2�Ĵ�С��ϵΪ��a2+b2��c2
��2��
�⣺��ͼ3������A��AD��BC�ڵ�D
��3��
�⣺֤������ͼ3����CD=x��
��Rt��ADC��AD2=b2��x2����Rt��ADB��AD2=c2����a+x��2
��a2+b2=c2��2ax
��a��0��x��0
��2ax��0
��a2+b2��c2
�൱��ABCΪ�۽�������ʱ��a2+b2��c2
����������1����������ɲ²⣺����ABCΪ�۽�������ʱ��a2+b2��c2�Ĵ�С��ϵΪ��a2+b2��c2����2������������������ߣ�����A��AD��BC�ڵ�D����3��Ȼ����CD=x���ֱ���Rt��ADC��Rt��ADB�У���ʾ��AD2 �� ����֤�ý��ۣ��������������ε��ۺ��⣮�����˹��ɶ����Լ������ε�������⣮ע�����������ǽ����Ĺؼ���
�����㾫����������Ĺؼ������������������߹�ϵ�����֪ʶ����������������֮�ʹ��ڵ����ߣ�����������֮��С�ڵ����ߣ������϶����������߶Σ�������������ε����ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P,Q�ֱ��DZ߳�Ϊ4 cm�ĵȱ�������ABC��AB,BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1 cm/s������AQ,CP���ཻ�ڵ�M.�����ĸ�������ȷ����________(�����).��BP=CM; �ڡ�ABQ �ա�CAP ;�ۡ�CMQ�Ķ������䣬ʼ�յ���60;�ܵ���![]() s��
s��![]() sʱ����PBQΪֱ��������.
sʱ����PBQΪֱ��������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һԪһ�η��̵ĸ���һԪһ�β���ʽ��Ľ⣬��Ƹ�һԪһ�η���Ϊ�ò���ʽ��Ĺ������̣�
��1���ڷ��̢�3x��1=0���� ![]() ��x��(3x+1)=��5 �У�������
��x��(3x+1)=��5 �У�������![]() �Ĺ���������________
����������________
��2��������ʽ��  ��һ���������̵ĸ��������� ������������̿�����________��д��һ�����ɣ�
��һ���������̵ĸ��������� ������������̿�����________��д��һ�����ɣ�
��3�������� 3��x=2x��3+x= ![]() ���ǹ��� x �IJ���ʽ��
���ǹ��� x �IJ���ʽ�� ![]() �Ĺ������̣�ֱ��д�� m ��ȡֵ��Χ.
�Ĺ������̣�ֱ��д�� m ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A(-1��5)��B��-1��0����C��-4��3����
�������ABC�������
������ͼ��������ABC����![]() ��ĶԳ�ͼ�Ρ�A1B1C1����д����A1��B1��C1�����꣮
��ĶԳ�ͼ�Ρ�A1B1C1����д����A1��B1��C1�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����A��B��C��ͬһֱ���ϣ�AB=2��BC=1���ֱ���AB��BCΪ�ߣ���ACͬ�����ȱ���ABD�͵ȱ���BCE���ֱ�����AE��CD.
��1���ҳ�ͼ�е�ȫ�������Σ������Ӹ����ߣ�����֤����Ľ���.

(2)�߶�AE���߶�CD�Ĺ�ϵ�ǣ�AE CD����>��=��<��.AE��CD�ļн��ǣ� .
(3) ��ABD�̶�������ʹ��BCE���ŵ�B��ת������ʱ��2���ó��Ľ��ۻ������𣨲�Ҫ��֤������
������ת�����У��߶�DC�ij��DZ仯�ģ����ı仯��Χ�� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��ͼ����x�ύ��A����1.0����B��3��0�����㣬��y�ύ�ڵ�C��0����3��������ΪD��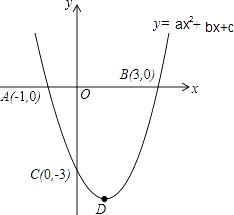
��1����������ߵĽ���ʽ��
��2����������߶���D������ͶԳ��ᣮ
��3��̽���Գ������Ƿ����һ��P��ʹ���Ե�P��D��AΪ������������ǵ��������Σ������ڣ���������з���������P������꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD��CB=CD���Խ���AC��BD�ཻ�ڵ�O�����н����У�
�١�ABC=��ADC��
��AC��BD�ƽ�֣�
��AC��BD�ֱ�ƽ���ı���ABCD������Խǣ�
���ı���ABCD�����S=![]() ACBD��
ACBD��
��ȷ���� ����д������ȷ���۵���ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ��Сѧ����ȫ�ͽ���������ijУ��֯�ˡ�����ˮ����ͨ��ȫ��������֪ʶ������Ϊ�����ھ����б�������İ༶��ѧУ����������Ʒ�̳�һ���Թ������ɸ����������ÿ������ļ۸���ͬ��ÿ������ļ۸���ͬ��������1�������1��������159Ԫ�����������۵�2����9Ԫ��
��1�������������ĵ��۸��Ƕ���Ԫ��
��2������ѧУʵ���������һ���Թ������������20������Ҫ���������������ܷ��ò�����1550Ԫ��ѧУ�����Թ�����ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��������һ���ı��εĿյ�![]() ����ͼ��ʾ���ּƻ��ڿյ�����ֲ��Ƥ��������
����ͼ��ʾ���ּƻ��ڿյ�����ֲ��Ƥ��������![]() ��AB=3m��BC=12m��CD=13m��DA=4m����ÿƽ���ײ�Ƥ��Ҫ200Ԫ����Ҫ����Ͷ�룿
��AB=3m��BC=12m��CD=13m��DA=4m����ÿƽ���ײ�Ƥ��Ҫ200Ԫ����Ҫ����Ͷ�룿

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com