
【题目】计算: ![]() +|1﹣
+|1﹣ ![]() |﹣2sin60°+(π﹣2016)0﹣
|﹣2sin60°+(π﹣2016)0﹣ ![]() .
.
【答案】解: ![]() +|1﹣
+|1﹣ ![]() |﹣2sin60°+(π﹣2016)0﹣
|﹣2sin60°+(π﹣2016)0﹣ ![]()
=3+ ![]() ﹣1﹣2×
﹣1﹣2× ![]() +1﹣2
+1﹣2
=3+ ![]() ﹣1﹣
﹣1﹣ ![]() +1﹣2
+1﹣2
=1.
【解析】本题涉及负整数指数幂、绝对值、特殊角的三角函数值、零指数幂、立方根5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、绝对值、特殊角的三角函数值、零指数幂、立方根等考点的运算.
【考点精析】根据题目的已知条件,利用零指数幂法则和整数指数幂的运算性质的相关知识可以得到问题的答案,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为 ,线段AD、BE之间的关系 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①请判断∠AEB的度数,并说明理由;②当CM=5时,AC比BE的长度多6时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点A、B、C在同一直线上,AB=2,BC=1,分别以AB、BC为边,在AC同侧作等边△ABD和等边△BCE,分别联结AE、CD.
(1)找出图中的全等三角形(不添加辅助线),并证明你的结论.

(2)线段AE与线段CD的关系是:AE CD(填>、=、<).AE与CD的夹角是: .
(3) △ABD固定不动,使△BCE绕着点B旋转,①这时(2)得出的结论还成立吗(不要求证明)?
②在旋转过程中,线段DC的长是变化的,它的变化范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m) 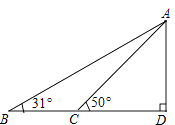
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,对角线AC,BD相交于点O,下列结论中:
①∠ABC=∠ADC;
②AC与BD相互平分;
③AC,BD分别平分四边形ABCD的两组对角;
④四边形ABCD的面积S=![]() ACBD.
ACBD.
正确的是 (填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=4,∠B=∠C=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BAD=20°时,∠EDC= °;
(2)当DC等于多少时,△ABD≌△DCE?试说明理由;
(3)△ADE能成为等腰三角形吗?若能,请直接写出此时∠BAD的度数;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:① EF=BE+CF;②∠BGC=90°+![]() ∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则
∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则![]() =mn. 其中正确的结论有( )
=mn. 其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com