
【题目】如图,△ABC中,AB=AC=4,∠B=∠C=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BAD=20°时,∠EDC= °;
(2)当DC等于多少时,△ABD≌△DCE?试说明理由;
(3)△ADE能成为等腰三角形吗?若能,请直接写出此时∠BAD的度数;若不能,请说明理由.

【答案】(1)20;(2)证明见解析;(3)证明见解析.
【解析】
试题(1)利用三角形的外角的性质得出答案即可;
(2)利用∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC得出∠BAD=∠EDC,进而求出△ABD≌△DCE;
(3)由等腰三角形的判定以及分类讨论得出即可.
试题解析:解:(1)∵∠BAD=20°,∠B=40°,∴∠ADC=60°,∵∠ADE=40°,∴∠EDC=60°﹣40°=20°,故答案为:20;
(2)当DC=2时,△ABD≌△DCE;理由:
∵∠ADE=40°,∠B=40°,又∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC,∴∠BAD=∠EDC.在△ABD和△DCE中,∵∠B=∠C,AB=DC,∠BAD=∠EDC,∴△ABD≌△DCE(ASA);
(3)当∠BAD=30°时,∵∠B=∠C=40°,∴∠BAC=100°,∵∠ADE=40°,∠BAD=30°,∴∠DAE=70°,∴∠AED=180°﹣40°﹣70°=70°,∴DA=DE,这时△ADE为等腰三角形;
当∠BAD=60°时,∵∠B=∠C=40°,∴∠BAC=100°,∵∠ADE=40°,∠BAD=60°,∠DAE=40°,∴EA=ED,这时△ADE为等腰三角形.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中装有一红一白2个球,这些球除颜色外都相同,小刚从袋中随机摸出一个球,记下颜色后放回袋中,再从袋中随机摸出一个球,两次都摸到红球的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
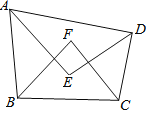
【题目】如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=70°,则∠ABC+∠BCD= ______ °;∠E= ______ °;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F,所添加的条件为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能够使△BPE与△CQP全等;此时点Q的运动速度为多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=50°,P为△ABC内一点,过点P的直线MN分別交AB、BC于点M、N.若M在PA的中垂线上,N在PC的中垂线上,则∠APC的度数为____________°

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com