[题目]在一个不透明的袋中装有一红一白2个球.这些球除颜色外都相同.小刚从袋中随机摸出一个球.记下颜色后放回袋中.再从袋中随机摸出一个球.两次都摸到红球的概率是．题目和参考答案——青夏教育精英家教网—

【题目】在一个不透明的袋中装有一红一白2个球，这些球除颜色外都相同，小刚从袋中随机摸出一个球，记下颜色后放回袋中，再从袋中随机摸出一个球，两次都摸到红球的概率是．

【答案】
【解析】解：画树状图得：

∵共有4种等可能的结果，两次都摸到红球的1种情况，
∴两次都摸到红球的概率是，
故答案为．
先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次都摸到红球的情况，再利用概率公式即可求得答案．此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；解题时要注意此题是放回实验还是不放回实验．用到的知识点为：概率=所求情况数与总情况数之比．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论的个数是（）

A.2
B.3
C.4
D.5

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为解决都匀市停车难的问题，计划在一段长为56米的路段规划处如图所示的停车位，已知每个车位是长为5米，宽为2米的矩形，且矩形的宽与路的边缘成45°角，则该路段最多可以划出个这样的停车位．（取 =1.4，结果保留整数）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE，则∠AEB的度数为　　，线段AD、BE之间的关系　　．

（2）拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．①请判断∠AEB的度数，并说明理由；②当CM=5时，AC比BE的长度多6时，求AE的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，△ABC中BA=BC，点D是AB延长线上一点，DF⊥AC于F交BC于E，

求证：△DBE是等腰三角形．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图，点A、B、C在同一直线上，AB=2，BC=1，分别以AB、BC为边，在AC同侧作等边△ABD和等边△BCE，分别联结AE、CD.

（1）找出图中的全等三角形（不添加辅助线），并证明你的结论.

(2)线段AE与线段CD的关系是：AE CD（填>、=、<）.AE与CD的夹角是： .

(3) △ABD固定不动，使△BCE绕着点B旋转，①这时（2）得出的结论还成立吗（不要求证明）？

②在旋转过程中，线段DC的长是变化的，它的变化范围是 .

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s，在一条笔直公路BD的上方A处有一探测仪，如平面几何图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°（tan31°≈0.6，tan50°≈1.2，结果精确到1m）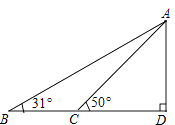

（1）求B，C的距离．
（2）通过计算，判断此轿车是否超速．