
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为 ,线段AD、BE之间的关系 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①请判断∠AEB的度数,并说明理由;②当CM=5时,AC比BE的长度多6时,求AE的长.

【答案】(1)60°;相等;(2)①∠AEB=90°;②AE= 17.
【解析】
(1)易证∠ACD=∠BCE,即可求证△ACD≌△BCE,根据全等三角形对应边相等可求得AD=BE,根据全等三角形对应角相等即可求得∠AEB的大小;
(2)易证△ACD≌△BCE,利用勾股定理进行解答即可.
解:(1)∵∠ACB=∠DCE,∠DCB=∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
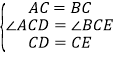 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CEB=∠ADC=180°﹣∠CDE=120°,
∴∠AEB=∠CEB﹣∠CED=60°,
故答案为:60°;相等;
(2)①∠AEB=90°,
∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
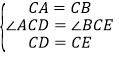 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC.
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°,
∵点A、D、E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=90°.
②∵CD=CE,CM⊥DE,
∴DM=ME=5.
在Rt△ACM中,AM2+CM2=AC2,
设:BE=AD=x,则AC=(6+x),
(x+5)2+52=(x+6)2,
解得:x=7.
所以可得:AE=AD+DM+ME=17.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点. 
(1)求证:CP=AQ;
(2)若BP=1,PQ=2 ![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中装有一红一白2个球,这些球除颜色外都相同,小刚从袋中随机摸出一个球,记下颜色后放回袋中,再从袋中随机摸出一个球,两次都摸到红球的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com