
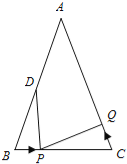
����Ŀ����ͼ����֪��ABC �У�AB=AC=6cm����B=��C��BC=4cm���� D Ϊ AB���е㣮
��1������� P ���߶� BC ���� 1cm/s ���ٶ��ɵ� B ��� C �˶���ͬʱ���� Q ���߶� CA ���ɵ� C ��� A �˶���
������ Q ���˶��ٶ���� P ���˶��ٶ���ȣ����� 1 �����BPD ����CQP �Ƿ�ȫ�ȣ���˵�����ɣ�
������ Q ���˶��ٶ���� P ���˶��ٶȲ���ȣ����� Q ���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD ����CQP ȫ�ȣ�
��2������ Q �Ԣ��е��˶��ٶȴӵ� C �������� P ��ԭ�����˶��ٶȴӵ� B ͬʱ����������ʱ���ء�ABC �����˶����� �� P ��� Q ��һ���ڡ�ABC �� �������������ں�����ֱ��д���𰸣�������д������̣�

���𰸡���1����ȫ�ȣ����ɼ�������1��5cm/s���ɼ�������2��24s����AC������
��������
���⣨1��������ʱ����ٶȷֱ����������������BP��CQ��BD��PC�ߵij�������SAS�ж�����������ȫ�ȣ�
������ȫ��������Ӧ���������̽���֮��Ĺ�ϵ���ٸ���·��=�ٶ���ʱ�乫ʽ������õ�P�˶���ʱ�䣬����õ�Q���˶��ٶȣ�
��2������������ͼ�η������֣����ڵ�Q���ٶȿ죬���ڵ�P��ǰ�ߣ�����Ҫ���һ����������Ӧ�ñȵ�P���ߵ��������ε������߳���
�⣺��1����ȫ�ȣ��������£�
��t=1�룬
��BP=CQ=1��1=1���ף�
��AB=6cm����DΪAB���е㣬
��BD=3cm��
����PC=BC��BP��BC=4cm��
��PC=4��1=3cm��
��PC=BD��
����AB=AC��
���B=��C��
���BPD�ա�CQP��
��������BPD�ա�CQP��
��vP��vQ��
��BP��CQ��
���ߡ�BPD�ա�CQP����B=��C����BP=CP=2��BD=CQ=3��
����P����Q�˶���ʱ��t=![]() =2�룬
=2�룬
��vQ=![]() ==1.5cm/s��
==1.5cm/s��
��2���辭��x����P���Q��һ��������
�����⣬�� 1.5x=x+2��6��
���x=24��
����P���˶���24s��1cm/s=24cm��
��24=2��12��
����P����Q��AC����������
������24���P���Q��һ���ڱ�AC��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˾��С��ij������Ӫ��ȫ���ڶ�������Ĵ������ʻ�ģ�����涨��Ϊ�����г���̣���λ��km�����£�
+11�� -2�� +3�� +9�� -11�� +5�� -15�� -8
��1���������һ���˿��͵�Ŀ�ĵ�ʱ��С����������ص�ľ���Ϊ���٣�
��2����ÿǧ��Ӫ�˶�Ϊ5Ԫ���ɱ�Ϊ2.7Ԫ/km��������������ӯ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е���ʽ�����й�����3x��![]() �����������е�10������ʽӦ��
�����������е�10������ʽӦ��![]() ����
����![]()
A. 39x10 B. -39 x10 C. -43 x10 D. 43 x10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��֤����ƽ�澵������ߵĹ����ǣ��䵽ƽ�澵�ϵĹ��ߺͱ�������Ĺ�����ƽ�澵���е������ȣ�
��1����ͼ��һ������![]() �䵽ƽ�澵
�䵽ƽ�澵![]() �ϣ���
�ϣ���![]() ���䵽ƽ�澵
���䵽ƽ�澵![]() �ϣ��ֱ�
�ϣ��ֱ�![]() ���䣬����
���䣬����![]() ������Ĺ���
���������![]() �����
�����![]() ƽ�У���
ƽ�У���![]() ����
����![]() _________��
_________��![]() ________��
________��
��2���ڣ�1���У���![]() ����
����![]() _______����
_______����![]() ����
����![]() ________��
________��
��3���ɣ�1������2����������룺����ƽ�澵![]() ��
��![]() �ļн�
�ļн�![]() ________ʱ������ʹ�κ��䵽ƽ�澵
________ʱ������ʹ�κ��䵽ƽ�澵![]() �ϵĹ���
�ϵĹ���![]() ������ƽ�澵
������ƽ�澵![]() ��
��![]() ���������������
�����η�����������![]() �뷴�����
�뷴�����![]() ƽ�У���˵�����ɣ�
ƽ�У���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=8����BAD=60�㣬��E�ӵ�A��������AB��ÿ��2����λ���ȵ��ٶ����յ�B�˶�������E�����A�غ�ʱ������E��EF��AD�ڵ�F����EG��AD��AC�ڵ�G������G��GH��AD��AD����AD���ӳ��ߣ��ڵ�H���õ�����EFHG�����E�˶���ʱ��Ϊt��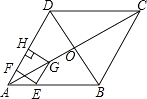
��1�����߶�EF�ij����ú�t�Ĵ���ʽ��ʾ����
��2�����H���D�غ�ʱt��ֵ��
��3�������EFHG������ABCD�ص�����ͼ�ε������Sƽ����λ����S��t֮��ĺ�����ϵʽ��
��4������EFHG�ĶԽ���EH��FG�ཻ�ڵ�O�䣬��OO���ADʱ��t��ֵΪ����OO���ADʱ��t��ֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ϲ����ж���ʽ�е�ͬ���
��1��3x2+4x��2x2��x+x2��3x��1��
��2����a2b+2a2b��
��3��a3��a2b+ab2+a2b��2ab2+b3��
��4��2a2b+3a2b��![]() a2b
a2b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ѧ���������ij˷���֪��23=8��25=32��������ʦ����û��20��2��3������У����ڶ��٣���ʦ������ʾ����25��23=4��25��3=4����25��23=25��3=22=4������Ŷ�����������ˣ���С��˵�����Һܿ�����˴𰸣��װ���ͬѧ�������������
��1���������ʦ�ķ����������20��2��3��ֵ��
��2���ݴ˱Ƚϣ���3����2�루��2����3�Ĵ�С����д��������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
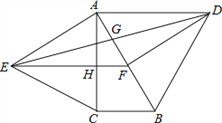
����Ŀ����ͼ���ֱ���ֱ�ǡ�ABC��б��AB��ֱ�DZ�ACΪ�����ABC�����ȱߡ�ABD�͵ȱߡ�ACE��FΪAB���е㣬DE��AB���ڵ�G��EF��AC���ڵ�H����ACB=90�㣬��BAC=30�㣮�������½��ۣ�
��EF��AC�� ���ı���ADFEΪ���Σ� ��AD=4AG�� ��FH=![]() BD
BD
������ȷ�Ľ����У� ����
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
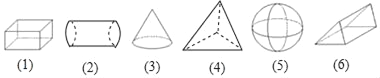
����Ŀ��������д�����м����壬��������࣮��ֻ��д��ţ�
������������������������֣�������_____������_____������_____��
��������������������֣����������_____�����������_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com