
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、b满足|a+2|+(c﹣7)2=0. ![]()
(1)a= , b= , c=;
(2)若将数轴折叠,使得A点与C点重合,则点B与数表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= , AC= , BC= . (用含t的代数式表示)
(4)请问:3BC﹣2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】
(1)-2;1;7
(2)4
(3)3t+3;5t+9;2t+6
(4)解:不变.
3BC﹣2AB=3(2t+6)﹣2(3t+3)=12
【解析】解:(1)∵|a+2|+(c﹣7)2=0,
∴a+2=0,c﹣7=0,
解得a=﹣2,c=7,
∵b是最小的正整数,
∴b=1;
所以答案是:﹣2,1,7.(2)(7+2)÷2=4.5,
对称点为7﹣4.5=2.5,2.5+(2.5﹣1)=4;
所以答案是:4.(3)AB=t+2t+3=3t+3,AC=t+4t+9=5t+9,BC=2t+6;
所以答案是:3t+3,5t+9,2t+6.
【考点精析】通过灵活运用数轴和两点间的距离,掌握数轴是规定了原点、正方向、单位长度的一条直线;同轴两点求距离,大减小数就为之.与轴等距两个点,间距求法亦如此.平面任意两个点,横纵标差先求值.差方相加开平方,距离公式要牢记即可以解答此题.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式:
13+23= ![]() ×4×9=
×4×9= ![]() ×22×32
×22×32
13+23+33=36= ![]() ×9×16=
×9×16= ![]() ×32×42
×32×42
13+23+33+43=100= ![]() ×16×25=
×16×25= ![]() ×42×52
×42×52
(1)计算:13+23+33+43+…+103的值;
(2)猜想:13+23+33+43+…+n3的值.
(3)计算:513+523+533+…+993+1003的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把△ABC经过平移得到△A′B′C′,若A(1,m),B(4,2),点A的对应点A′(3,m+2),则点B对应点B′的标为( )
A. (6,5)B. (6,4)C. (5,m)D. (6,m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路,若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是
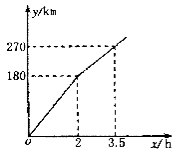
A. 汽车在高速公路上行驶速度为100km/h
B. 乡村公路总长为90km
C. 汽车在乡村公路上行驶速度为60km/h
D. 该记者在出发后4.5h到达采访地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天小明和冬冬利用温差来测量山峰的高度.冬冬在山脚测得的温度是8℃,小明此时在山顶测得的温度是2℃,已知该地区高度每升高80米,气温下降0.5℃,问这个山峰有多高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com