

分析 (1)根据等腰三角形性质和勾股定理解答即可;
(2)根据直角三角形面积求出PD×DC×$\frac{1}{2}$=15即可求出t;
(3)根据题意列出PD、MD的表达式,由于M在D点左右两侧情况不同,所以进行分段讨论即可,注意约束条件.
解答 解:(1)如图1,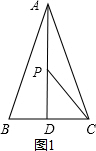
∵AB=AC=13,AD⊥BC,
∴BD=CD=5cm,且∠ADB=90°,
∴AD2=AC2-CD2
∴AD=12cm.
(2)如图2,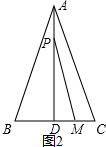
由题意可得:AP=t,PD=12-t,
又∵由△PDM面积为:$\frac{1}{2}$PD×DC=15,
解得:PD=6,
∴t=6.
(3)假设存在t,使得PM=AP+BM.
①若点M在线段CD上,如图3,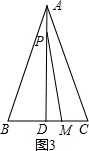
即 0≤t≤$\frac{5}{2}$时,AP=t,PD=12-t,DM=5-2t,BM=10-2t
则PM=$\sqrt{P{D}^{2}+D{M}^{2}}$=$\sqrt{(12-t)^{2}+(5-2t)^{2}}$,
故$\sqrt{(12-t)^{2}+(5-2t)^{2}}$=t+10-2t
整理得:4t2-24t+69=0,
△=b2-4ac=-528<0,故此方程无解;
②如图4,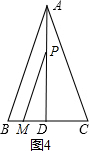
若点M在线段DB上,即 $\frac{5}{2}$<t≤5,
AP=t,PD=12-t,DM=2t-5,BM=10-2t,
则PM=$\sqrt{P{D}^{2}+D{M}^{2}}$=$\sqrt{(12-t)^{2}+(2t-5)^{2}}$,
故$\sqrt{(12-t)^{2}+(2t-5)^{2}}$=t+10-2t
整理得:4t2-24t+69=0,
△=b2-4ac=-528<0,故此方程无解;
③如图5,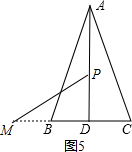
若点M在射线DB上,即 5<t≤12,
AP=t,PD=12-t,DM=2t-5,BM=2t-10,
PM=$\sqrt{M{D}^{2}+P{D}^{2}}$=$\sqrt{(2t-5)^{2}+(12-t)^{2}}$,
则$\sqrt{(2t-5)^{2}+(12-t)^{2}}$=t+2t-10,
整理得:
4t2-24t-69=0
解得t1=$\frac{6-\sqrt{105}}{2}$(舍去),t2=$\frac{6+\sqrt{105}}{2}$,
故当t=$\frac{6+\sqrt{105}}{2}$,使得PM=AP+BM.
点评 此题主要考查了三角形综合以及勾股定理等知识,此题关键为利用三角形性质勾股定理以及分段讨论,在解方程时,注意解是否符合约束条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
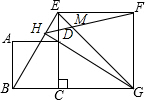 如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.
如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
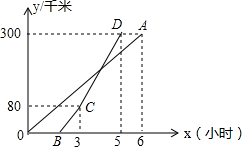 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题:
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
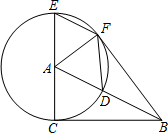 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com