Question

如图所示，AB∥CD，AD∥BC，BE＝DF，则图中全等三角形共有________对.

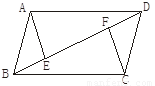
A.2                 B.3                 C.4                 D.5

 

Answer 1

【答案】

B

【解析】

试题分析：先证明四边形ABCD是平行四边形，根据平行四边形的对角线把平行四边形分成两个全等的三角形，再利用BE=DF可以证明△ABE≌△CDF，同理可证△AED≌△CFB．

①∵AB∥CD，AD∥BC，

∴四边形ABCD是平行四边形，

∴ABD≌△CDB；

②∵AB∥CD，

∴∠ABD=∠CDB，

在△ABE和△CDF中，

AB=CD，∠ABD=∠CDB，BE=DF

∴△ABE≌△CDF（ASA）；

③∵BE=DF，

∴BE+EF=DF+EF，

即BF=DE，

同理可证△AED≌△CFB；

所以图中全等三角形共有3对．

故选B．

考点：本题主要考查全等三角形的判定

点评：先根据平行证明四边形为平行四边形，再利用平行四边形的性质是解答本题的前提，也是解答本题的突破口和关键．做题时从已知开始结合全等的判定方法由易到难逐个找寻．