
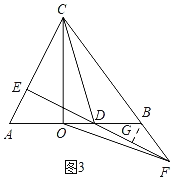
【题目】如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6.
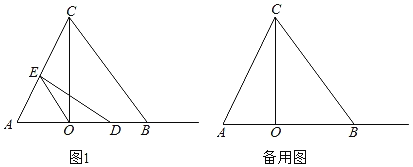
(1)求BC,AC的长;
(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.
①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.
②设DE交直线BC于点F,连结OF,CD,若S△OBF:S△OCF=1:4,则CD的长为 (直接写出结果).
【答案】(1)4![]() ;(2)
;(2)![]() 或8
或8![]() .
.
【解析】
根据BA=BC,分别用勾股定理求出CO和AC的长.
①分情况AO=OE和AO=AE,画出图形,根据三角形中位线定理和证明三角形全等解决问题.
②分情况
i)当D在线段OB上时,如图3,过B作BG⊥EF于G,根据同高三角形面积比等于底边之比,得到![]() ,再根据平行线性质∠BDG=∠BFG,得到BD=BF=
,再根据平行线性质∠BDG=∠BFG,得到BD=BF=![]() ,最后使用勾股定理求出结论
,最后使用勾股定理求出结论
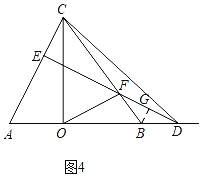
ii)当D在线段OB的延长线上时,如图4,过B作BG⊥DE于G,同理计算可得结论.
解:(1)∵AO=4,BO=6,
∴AB=10,
∵BA=BC,
∴BC=10,
∵CO⊥AB,
∴∠AOC=∠BOC=90°,
由勾股定理得:CO=![]() =
=![]() =8,
=8,
AC=![]() =
=![]() =4
=4![]() ;
;
(2)①分两种情况:
i)如图1,当AO=OE=4时,过O作ON⊥AC于N,
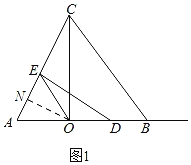
∴AN=EN,
∵DE⊥AC,
∴ON∥DE,
∴AO=OD=4;
ii)当AO=AE=4时,如图2,
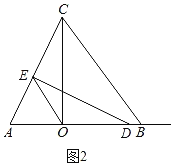
在△CAO和△DAE中,
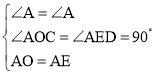 ,
,
∴△CAO≌△DAE(AAS),
∴AD=AC=4![]() ,
,
∴OD=4![]() ﹣4;
﹣4;
②分两种情况:
i)当D在线段OB上时,如图3,过B作BG⊥EF于G,
∵S△OBF:S△OCF=1:4,
∴![]()
∴![]()
∵CB=10
∴BF=![]()
∵EF⊥AC,
∴BG∥AC,
∴∠GBF=∠ACB,
∵AE∥BG,
∴∠A=∠DBG,
∵AB=BC,
∴∠A=∠ACB,
∴∠DBG=∠GBF,
∵∠DGB=∠FGB,
∴∠BDG=∠BFG,
∴BD=BF=![]() ,
,
∴OD=OB﹣BD=6﹣![]() =
=![]() ,
,
∴CD=![]() =
=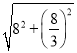 =
=![]() ;
;
ii)当D在线段OB的延长线上时,如图4,过B作BG⊥DE于G,
同理得![]() ,
,
∵BC=10,
∴BF=2,
同理得:∠BFG=∠BDF,
∴BD=BF=2,
Rt△COD中,CD=![]() =
=![]() =8
=8![]() ,
,
综上,CD的长为![]() 或8
或8![]() .
.
故答案为:![]() 或8
或8![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】仙降是瑞安重要的制鞋基地,其生产的鞋子畅销世界各地,某制鞋企业欲将![]() 件产品运往
件产品运往![]() 三地销售,运往
三地销售,运往![]() 地的费用为18元/件,运往
地的费用为18元/件,运往![]() 地的费用为20元/件,运往
地的费用为20元/件,运往![]() 地的费用为17元/件,要求运往
地的费用为17元/件,要求运往![]() 地的件数与运往
地的件数与运往![]() 地的件数相同. 设安排
地的件数相同. 设安排![]() 件产品运往
件产品运往![]() 地.
地.
(1)若![]() ①运往
①运往![]() 地件数为 件(用含
地件数为 件(用含![]() 的代数式表示);②若总运费不超过1850元,则运往
的代数式表示);②若总运费不超过1850元,则运往![]() 地至少有多少件?
地至少有多少件?
(2)若总运费为1900元,则![]() 的最大值为 .(直接写出答案)
的最大值为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,点E是CD上一点,AE平分∠BAD,BF平分∠ABC,延长BE交AD的延长线于点F
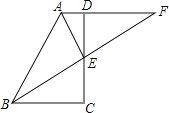
(1)求证:△ABE≌△AFE;
(2)若AD=2,BC=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.

(1)求证:△BCF≌△DCE;
(2)若BC=5,CF=3,∠BFC=90°,求DG︰GC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,点
,点![]() 在该函数的图象上,点
在该函数的图象上,点![]() 到
到![]() 轴、
轴、![]() 轴的距离分别为
轴的距离分别为![]() 、
、![]() .设
.设![]() ,下列结论中:
,下列结论中:
①![]() 没有最大值;②
没有最大值;②![]() 没有最小值;③
没有最小值;③![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
④满足![]() 的点
的点![]() 有四个.其中正确结论的个数有( )
有四个.其中正确结论的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对应点为
的对应点为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,顶点
,顶点![]() 在直线
在直线![]() 上.
上.

![]() 证明四边形
证明四边形![]() 是菱形,并求点
是菱形,并求点![]() 的坐标;
的坐标;
![]() 求抛物线的对称轴和函数表达式;
求抛物线的对称轴和函数表达式;
![]() 在抛物线上是否存在点
在抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等?若存在,直接写出点
的面积相等?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 与x、y轴分别交于A、B两点,
与x、y轴分别交于A、B两点,![]() 与x、y轴交于C、D两点.
与x、y轴交于C、D两点.
(1)求A、B、C、D的坐标(用含k、m的代数式表示);
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在(2)的前提下,若![]() 的面积为27,求m的值.
的面积为27,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() .
.
![]() 当抛物线的顶点在
当抛物线的顶点在![]() 轴上时,求该抛物线的解析式;
轴上时,求该抛物线的解析式;
![]() 不论
不论![]() 取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
取何值时,抛物线的顶点始终在一条直线上,求该直线的解析式;
![]() 若有两点
若有两点![]() ,且该抛物线与线段
,且该抛物线与线段![]() 始终有交点,请直接写出
始终有交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com