
【题目】如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.

(1)求证:△BCF≌△DCE;
(2)若BC=5,CF=3,∠BFC=90°,求DG︰GC的值.
【答案】(1)证明见解析(2)4:3
【解析】
(1)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°………………………………………………1分
∵△ECF是等腰直角三角形,CE=CF
∴∠FCE=90°
∴∠BCF+∠FCD=∠ECD+∠FCD=90°
∴∠BCF=∠ECD…………………………………………………………3分
∴△BCF≌△DCE;……………………………………………………4分
(2)在Rt△BCF中,∠BFC=90°
∴BF=![]() ……………………………………………5分
……………………………………………5分
∵△BCF≌△DCE
∴DE=BC=4,∠CED=90°
∵△ECF是等腰直角三角形,CE=CF
∴∠CFE=∠CEF=∠DEF=45°………………………………………6分
∵∠CGF=∠DGE
∴△CGF∽△DGE………………………………………………………7分
∴![]() ……………………………………………………8分
……………………………………………………8分
(1)根据四边形ABCD是正方形,可得∠BCF+∠FCD=90°,BC=CD.根据△ECF是等腰直角三角形,CF=CE,可知∠ECD+∠FCD=90度.所以∠BCF=∠ECD.所以△BCF≌△DCE.
(2)在Rt△BFC中,BF=![]() ,所以可知DE=BF=4,∠BFC=∠DEC=∠FCE=90度.得到DE∥FC.可证明△DGE∽△CGF.所以DG:GC=DE:CF=4:3.
,所以可知DE=BF=4,∠BFC=∠DEC=∠FCE=90度.得到DE∥FC.可证明△DGE∽△CGF.所以DG:GC=DE:CF=4:3.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
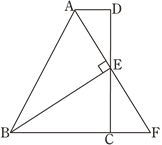
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰△ABC中,AB=AC,∠ABC的平分线交AC于D,过点A作AE // BC交BD的延长线于点E,∠CAE的平分线交BE于点F.
(1)①如图,若∠BAC=36o,求证:BD=EF;
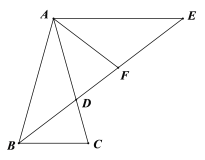
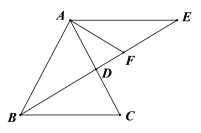
②如图,若∠BAC=60o,求![]() 的值;
的值;
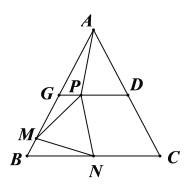
(2)如图,若∠BAC=60o,过点D作DG// BC,交AB于点G,点N为BC中点,点P, M分别是GD, BG上的动点,且∠PNM=60°. 求证:AP=PN=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海上有一灯塔P,在它周围3海里处有暗礁.一艘客轮以9海里/时的速度由西向东航行,行至A点处测得P在它的北偏东60度的方向,继续行驶20分钟后,到达B处又测得灯塔P在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+2的图象经过点A,且y随x的增大而减小.则A点的坐标可以是( )
A.(2,5)B.(﹣1,1)C.(3,0)D.(![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
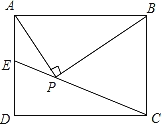
【题目】如图,长方形ABCD中,AB=4,AD=3,长方形内有一个点P,连结AP,BP,CP,已知∠APB=90°,CP=CB,延长CP交AD于点E,则AE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BA=BC,CO⊥AB于点O,AO=4,BO=6.
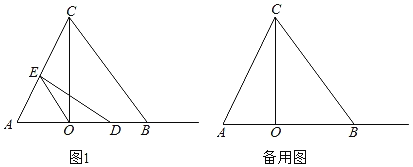
(1)求BC,AC的长;
(2)若点D是射线OB上的一个动点,作DE⊥AC于点E,连结OE.
①当点D在线段OB上时,若△AOE是以AO为腰的等腰三角形,请求出所有符合条件的OD的长.
②设DE交直线BC于点F,连结OF,CD,若S△OBF:S△OCF=1:4,则CD的长为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.

A. 1 B. 1或3 C. 1或7 D. 3或7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com