
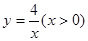 经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与
经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与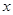 轴正半轴的夹角 ,AB∥
轴正半轴的夹角 ,AB∥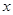 轴,将△ABC翻折后,得△
轴,将△ABC翻折后,得△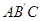 ,
,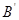 点落在OA上,则四边形OABC的面积为 .
点落在OA上,则四边形OABC的面积为 .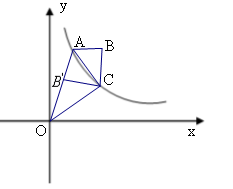
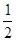 xy,则S△OCB′=
xy,则S△OCB′=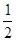 xy,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=6,从而得出三角形ABC的面积等于
xy,由AB∥x轴,得点A(x-a,2y),由题意得2y(x-a)=6,从而得出三角形ABC的面积等于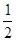 ay,即可得出答案.
ay,即可得出答案.
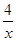 (x>0)经过四边形OABC的顶点A、C,
(x>0)经过四边形OABC的顶点A、C,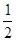 xy=2,
xy=2,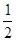 xy=2,
xy=2,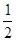 ay=1,
ay=1,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:单选题
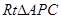 的顶点A,P在反比例函数
的顶点A,P在反比例函数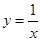 的图像上,已知P的坐标为(1,1),
的图像上,已知P的坐标为(1,1),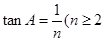 的自然数);当n=2,3,4…2010时,A的横坐标相应为
的自然数);当n=2,3,4…2010时,A的横坐标相应为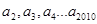 ,则
,则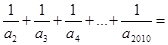 ( )
( )A.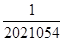 | B.2021054 | C.2022060 | D.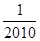 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com