
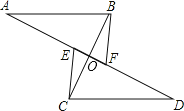
【题目】如图,AB∥CD,CE∥BF,
A. E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
A. 2
B. 3
C. 4
D. 5
【答案】B
【解析】分析已知和所求,先由CE∥BF,根据平行线性质得出内错角∠ECO=∠FBO,再由对顶角∠EOC=∠FOB和OE=OF,根据三角形的判定即可判定两个三角形全等;由上分析所得三角形全等,根据全等三角形的性质可得对应边相等,再根据三角形的判定定理即可判定另两对三角形是否全等.
①∵CE∥BF,
∴∠OEC=∠OFB,
又∵OE=OF,∠COE=∠BOF,
∴△OCE≌△OBF,
∴OC=OB,CE=BF;
②∵AB∥CD,
∴∠ABO=∠DCO,∠AOB=∠COD,
又∵OB=OC,
∴△AOB≌△DOC;
③∵AB∥CD,CE∥BF,
∴∠D=∠A,∠CED=∠COD,
又∵CE=BF,
∴△CDE≌△BAF.
故选B.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
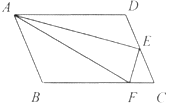
【题目】如图,在□ABCD中,点E是CD的中点,点F是BC边上的一点,且EF⊥AE.求证:AE平分∠DAF.
小林同学读题后有一个想法,延长FE,AD交于点M,要证AE平分∠DAF,只需证△AMF是等腰三角形即可.请你参考小林的想法,完成此题的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 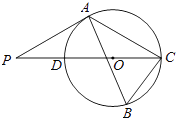
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,已知AB=DE,∠A=∠D,若要得到△ABC≌△DEF,则还要补充一个条件,在下列补充方法:①AC=DF;②∠B=∠E;③∠B=∠F;④∠C=∠F ⑤BC=EF中,则错误结论的序号是__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):
表示立方米):
价目表 | |
每月用水量 | 单价 |
不超出 |
|
超出 |
|
超出 |
|
注:水费按月结算 | |
例:若某户居民![]() 月份用水
月份用水![]() ,应收水费为
,应收水费为![]() (元).
(元).
请根据上表的内容解答下列问题:
![]() 填空:若该户居民
填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费________元;
,则应收水费________元;
![]() 若该户居民
若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?(用含
),则应收水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
![]() 若该户居民
若该户居民![]() ,
,![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() ,
,![]() 两个月共交水费多少元?(用含
两个月共交水费多少元?(用含![]() 的表示,并化简)
的表示,并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由“※”组成的图案和算式,解答问题:
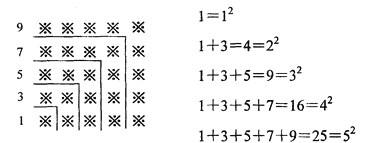
(1)请猜想1+3+5+7+9+…+19=_______________________;
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1) =___________;
(3)请用上述规律计算:51+53+55+…+2011+2013.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A,B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= . 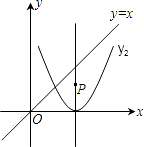
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com