
【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:

①AP=EF;②∠PFE=∠BAP;③PD=![]() EC;④△APD一定是等腰三角形.
EC;④△APD一定是等腰三角形.
其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AE与CD相交于点B,射线BF平分∠ABC,射线BG在∠ABD内,
(1)若∠DBE的补角是它的余角的3倍,求∠DBE的度数;
(2)在(1)的件下,若∠DBG=∠ABG﹣33°,求∠ABG的度数;
(3)若∠FBG=100°,求∠ABG和∠DBG的度数的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:在正方形ABCD中,以正方形的一个顶点A为顶点,且过对角顶点C的抛物线,称为这个正方形的以A为顶点的对角抛物线.
(1)在平面直角坐标系xOy中,点在轴正半轴上,点C在y轴正半轴上.
①如图1,正方形OABC的边长为2,求以O为顶点的对角抛物线;
②如图2,在平面直角坐标系xOy中,正方形OABC的边长为a,其以O为顶点的对角抛物线的解析式为y= ![]() x2 , 求a的值;
x2 , 求a的值;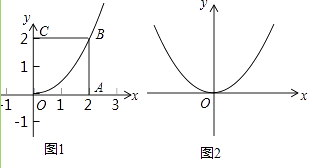
(2)如图3,正方形ABCD的边长为4,且点A的坐标为(3,2),正方形的四条对角抛物线在正方形ABCD内分别交于点M、P、N、Q,直接写出四边形MPNQ的形状和四边形MPNQ的对角线的交点坐标.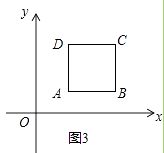
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,CE∥BF,
A. E、F、D在一直线上,BC与AD交于点O,且OE=OF,则图中有全等三角形的对数为( )
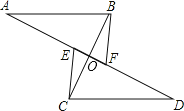
A. 2
B. 3
C. 4
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
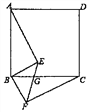
【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C,D是圆O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F.则下列结论:
①AD⊥BD;②∠AOC=∠ABC;③CB平分∠ABD;④AF=DF;⑤BD=2OF.
其中一定成立的是( )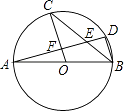
A.①③⑤
B.②③④
C.②④⑤
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
(1)求证:△ABD≌△CAE;
(2)若∠FBA=60°,连结DF、EF,判断△DEF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com