
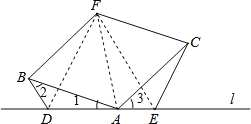
【题目】如图,已知四边形ABFC为菱形,点 D、A、E在直线l上,∠BDA=∠BAC=∠CEA.
(1)求证:△ABD≌△CAE;
(2)若∠FBA=60°,连结DF、EF,判断△DEF的形状,并说明理由.

【答案】(1)见解析;(2)△DEF是等边三角形,理由见解析
【解析】(1)利用菱形的性质得出AB=AC,进而得出∠2=∠3,即可利用AAS证明△ABD≌△CAE;
(2)易证△ABF与△ACF均为等边三角形,然后证明△FBD≌△FAE,则DF=EF,∠BFD=∠AFE,从而求得∠DFE的度数,即可证得:△DEF是等边三角形.
(1)证明:∵四边形ABFC为菱形,
∴AB=AC.
∵∠BDA=∠BAC=∠CEA,
又∵![]()
∴∠2=∠3.
在△ABD和△CAE中,
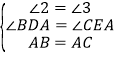
∴△ABD≌△CAE(AAS);
(2)答:△DEF是等边三角形.
连结AF,
∵四边形ABFC为菱形,![]()
∴△ABF与△ACF均为等边三角形,
∴BF=AF,![]()
∵∠2=∠3,
∴∠FBA+∠2=∠FAC+∠3,即∠FBD=∠FAE,
∵△ABD≌△CAE,
∴BD=AE.
在△FBD和△FAE中,
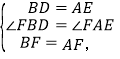
∴△FBD≌△FAE,
∴DF=EF,∠BFD=∠AFE.
∵![]()
∴![]() 即
即![]()
∴△DEF是等边三角形.


科目:初中数学 来源: 题型:
【题目】小明从A点出发向北偏东60°方向走了80m米到达B地,从B地他又向西走了160m到达C地.
(1)用1:4000的比例尺(即图上1cm等于实际距离40m)画出示意图,并标上字母;
(2)用刻度尺出AC的距离(精确到0.01cm),并求出C但距A点的实际距离(精确到1m);
(3)用量角器测出C点相对于点A的方位角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
求证:∠P=90°﹣![]() ∠C;
∠C;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.则不能使四边形ABCD成为矩形的是( )
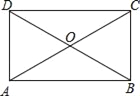
A. ①②③ B. ②③④ C. ②⑤⑥ D. ④⑤⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A,B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= . 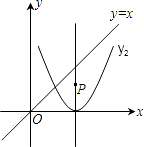
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校6km的郊外游玩,一部分同学步行,另一部分同学骑车。如图, ![]() 分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用的时间x(min)之间的函数图像,则下列判断错误的是
分别表示步行和骑车的同学前往目的地所走的路程y(km)与所用的时间x(min)之间的函数图像,则下列判断错误的是

A. 骑车的同学比步行的同学晚出发30min
B. 步行的同学的速度是6km/h
C. 骑车的同学从出发到追上步行的同学用了20min
D. 骑车的同学和步行的同学同时到达目的地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转得到△A1B1C,斜边A1B1与CB相交于点D,且DC=AC,则旋转角∠ACA1等于( ) 
A.20°
B.25°
C.30°
D.35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3). 
①若△ABC经过平移后得到△A1B1C1 , 已知点C1的坐标为(4,0),写出顶点A1 , B1的坐标;
②若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
③将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3 , 写出△A3B3C3的各顶点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com