
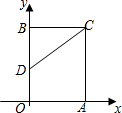
 在平面直角坐标系中,矩形OABC的顶点O在标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=6,OB=8,D为边OB的中点.
在平面直角坐标系中,矩形OABC的顶点O在标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=6,OB=8,D为边OB的中点.分析 (1)由于C、D是定点,则CD是定值,如果△CDE的周长最小,即DE+CE有最小值.为此,作点C关于x轴的对称点C′,当点E在线段C′D上时,△CDE的周长最小;
(2)由于DC、EF的长为定值,如果四边形CDEF的周长最小,即DE+FC有最小值.为此,作点D关于x轴的对称点D′,在CB边上截取CG=3,当点E在线段D′G上时,四边形CDEF的周长最小.
解答 解:(1)如图1,作点C关于x轴的对称点C′,连接C′D与x轴交于点E,连接CE.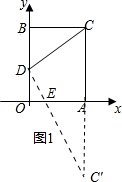
若在边OA上任取点E′(与点E不重合),连接CE′、DE′、C′E′,
由DE′+CE′=DE′+C′E′>C′D=C′E+DE,
可知△CDE的周长最小.
∵在矩形OACB中,OA=6,OB=8,D为边OB的中点,
∴BC=6,BD=OD=4,
∴点D(0,4),点C′(6,-8).
设直线C′D的解析式为y=kx+b(k≠0),
则$\left\{\begin{array}{l}{b=4}\\{6k+b=-8}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
∴直线C′D的解析式为y=-2x+4.
当y=-2x+4=0时,x=2,
∴点E的坐标为(2,0).
故答案为:(2,0).
(2)作点D关于x轴的对称点D′,在CB边上截取CG=3,连接D′E与x轴交于点E,在EA上截取EF=3,如图2所示.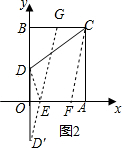
∵GC∥EF,GC=EF,
∴四边形GEFC为平行四边形,GE=CF.
又∵DC、EF的长为定值,
∴此时得到的点E、F使四边形CDEF的周长最小,
∵OE∥BC,
∴△D′OE∽△D′BG,
∴$\frac{OE}{BG}=\frac{D′O}{D′B}$,
BG=BC-CG=6-3=3,D′O=DO=4,D′B=D′O+OB=4+8=12,
∴OE=$\frac{D′O•BG}{D′B}$=$\frac{4×3}{12}$=1.
即点E的坐标为(1,0).
故答案为:(1,0).
点评 此题主要考查轴对称--最短路线问题,解决此类问题,一般都是运用轴对称的性质,将求折线问题转化为求线段问题,其说明最短的依据是三角形两边之和大于第三边.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (-7,4) | B. | (7,4) | C. | (2,1) | D. | (-1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某新建小区里安装了一架秋千,图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是(3-$\frac{3\sqrt{2}}{2}$)米.
某新建小区里安装了一架秋千,图是一个小孩荡秋千的侧面示意图,秋千的链子OA的长度为3米,秋千向两边摆动的最大角度相同,且最大角度的和∠BOC恰好为90°,则它摆至最高位置与最低位置的高度之差是(3-$\frac{3\sqrt{2}}{2}$)米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
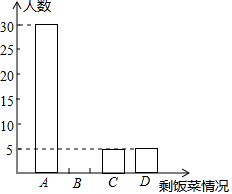 我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日午饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表和统计图,根据所提供的信息回答下列问题:| 选项 | 频数 | 频率 |
| A | 30 | m |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | 5 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 8$\sqrt{3}$cm | D. | 4$\sqrt{3}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com