

分析 (1)①过点C作CE⊥CB,与直线MN于点E,据此作图即可;
②先根据ASA判定△CAE≌△CDB,得出AE=DB,CE=CB,进而得到△ECB为等腰直角三角形,得出BE=$\sqrt{2}$CB,再根据BE=AE+AB,得到BE=BD+AB,即可得出BD+AB=$\sqrt{2}$CB;
(2)①过点C作CE⊥CB,与直线MN于点E,根据∠ACE=∠DCB,∠D=∠CAE,即可判定△ACE∽△DCB,进而得出$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,从而得到$\sqrt{3}$BE=2CB,$\sqrt{3}$AE=BD,最后根据AB=AE+BE,得出$\sqrt{3}$AB=$\sqrt{3}$AE+$\sqrt{3}$BE,即$\sqrt{3}$AB=BD+2CB;
②过点C作CE⊥CB,与直线MN于点E,根据∠ACE=∠DCB,∠D=∠CAE,判定△ACE∽△DCB,进而得出$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,即可得到$\sqrt{3}$BE=2CB,$\sqrt{3}$AE=BD,最后根据AB=AE-BE,得出$\sqrt{3}$AB=$\sqrt{3}$AE-$\sqrt{3}$BE,即$\sqrt{3}$AB=BD-2CB.
解答  解:(1)①补全图形如图1所示;
解:(1)①补全图形如图1所示;
②∵∠ACD=90°,CE⊥CB,
∴∠ECB=90°=∠ACD,
∴∠ACE=∠DCB.
∵DB⊥MN于点B,
∴∠ABD=90°,
∴∠BAC+∠D=180°.
又∵∠BAC+∠EAC=180°,
∴∠D=∠EAC.
在△CAE和△CDB中,
$\left\{\begin{array}{l}{∠ACE=∠DCB}\\{CA=CD}\\{∠EAC=∠D}\end{array}\right.$
∴△CAE≌△CDB,
∴AE=DB,CE=CB,
∴△ECB为等腰直角三角形,
∴BE=$\sqrt{2}$CB.
又∵BE=AE+AB,
∴BE=BD+AB,
即BD+AB=$\sqrt{2}$CB,
故答案为:BD+AB=$\sqrt{2}$CB;
(2)①证明:如图2,过点C作CE⊥CB,与直线MN于点E,
∵∠ACD=90°,CE⊥CB,
∴∠ECB=90°=∠ACD,
∴∠ACE=∠DCB.
∵DB⊥MN,
∴∠DBF=90°=∠ACF,
又∵∠DFB=∠AFC,
∴∠D=∠CAE,
∴△ACE∽△DCB,
又∵CD=$\sqrt{3}$AC,
∴$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,
∴Rt△BCE中,$\frac{CB}{BE}$=$\frac{\sqrt{3}}{2}$,即$\sqrt{3}$BE=2CB,
∵$\frac{BD}{EA}$=$\sqrt{3}$,
∴$\sqrt{3}$AE=BD,
∵AB=AE+BE,
∴$\sqrt{3}$AB=$\sqrt{3}$AE+$\sqrt{3}$BE,
即$\sqrt{3}$AB=BD+2CB;
②线段BD、AB、CB满足的数量关系是:BD-2CB=$\sqrt{3}$AB.
理由:如图3,过点C作CE⊥CB,与直线MN于点E,
∵∠ACD=90°,CE⊥CB,
∴∠ECB=90°=∠ACD,
∴∠ACE=∠DCB.
∵DB⊥MN,
∴∠DBA=90°=∠ACD,
又∵∠AFB=∠DFC,
∴∠D=∠CAE,
∴△ACE∽△DCB,
又∵CD=$\sqrt{3}$AC,
∴$\frac{CD}{CA}$=$\frac{CB}{CE}$=$\frac{BD}{EA}$=$\sqrt{3}$,
∴Rt△BCE中,$\frac{CB}{BE}$=$\frac{\sqrt{3}}{2}$,即$\sqrt{3}$BE=2CB,
∵$\frac{BD}{EA}$=$\sqrt{3}$,
∴$\sqrt{3}$AE=BD,
∵AB=AE-BE,
∴$\sqrt{3}$AB=$\sqrt{3}$AE-$\sqrt{3}$BE,
即$\sqrt{3}$AB=BD-2CB.
故答案为:$\sqrt{3}$AB=BD-2CB.
点评 本题属于三角形作图,主要考查了全等三角形的判定与性质,相似三角形的判定与性质以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形和相似三角形,运用全等三角形的对应边相等以及相似三角形的对应边成比例进行推导计算.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:填空题
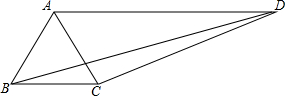 在四边形ABCD中,连接对角线AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,则BD=3$\sqrt{13}$.
在四边形ABCD中,连接对角线AC、BD,AB=BC,DC=6,AD=9,且∠ABC=2∠ADC=60°,则BD=3$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
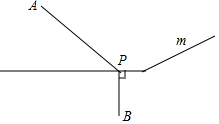 如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.
如图所示,在两个村庄A,B附近的河流可以近似地看成一条折线段(图中m)A,B分别在河的两旁,现要在河边修一个水泵站,同时向A,B两村供水,为了节约建设的费用,就要使所铺设的管道最短,某人甲提出了这样的建议:从点B向河道作垂线交m于点P,则点P为水泵站的位置.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
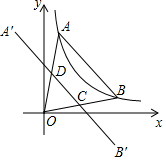 如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).
如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com