
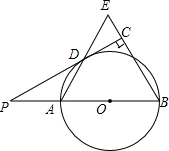
 如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE⊥PD,交PD的延长线于点C,连接AD并延长,交BE于点E.分析 (1)本题可连接OD,由PD切⊙O于点D,得到OD⊥PD,由于BE⊥PC,得到OD∥BE,得出∠ADO=∠E,根据等腰三角形的性质和等量代换可得结果;
(2)由(1)知,OD∥BE,得到∠POD=∠B,根据三角函数的定义即可得DC,OD的长,再由勾股定理可求出OC的长
解答 (1)证明:连接OD,
∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:∵OD∥BE,∠ABC=60°,
∴∠DOP=∠ABC=60°,
∵PD⊥OD,
∴tan∠DOP=$\frac{DP}{OD}$,
∴$\frac{2\sqrt{3}}{OD}=\sqrt{3}$,
∴OD=2,
∴OP=4,
∴PB=6,
∴sin∠ABC=$\frac{PC}{PB}$,
∴$\frac{\sqrt{3}}{2}=\frac{PC}{6}$,
∴PC=3$\sqrt{3}$,
∴DC=$\sqrt{3}$,
∴DC2+OD2=OC2,
∴($\sqrt{3}$)2+22=OC2,
∴OC=$\sqrt{7}$.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


科目:初中数学 来源: 题型:解答题
 2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH-60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
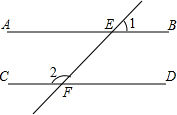 如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )
如图,AB∥CD,直线EF分别交直线AB,CD于点E,F,若∠1=46°,则∠2的度数为( )| A. | 44° | B. | 46° | C. | 134° | D. | 144° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届四川省广安市岳池县九年级第二次诊断考试数学试卷(解析版) 题型:填空题
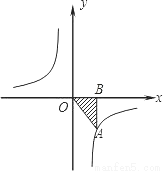
如图:点A在双曲线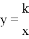 上,AB丄x轴于B,且△AOB的面积S△AOB=2,则k=__________.
上,AB丄x轴于B,且△AOB的面积S△AOB=2,则k=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com