
 已知在平面直角坐标系中,点A,B表示两个大型综合商场,坐标分别为A(2,-5),B(5,1).x轴,y轴分别表示庆春路和延安路,请在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出点C的坐标.
已知在平面直角坐标系中,点A,B表示两个大型综合商场,坐标分别为A(2,-5),B(5,1).x轴,y轴分别表示庆春路和延安路,请在同一个坐标系内画出满足下列条件的点(保留画图痕迹),并求出点C的坐标.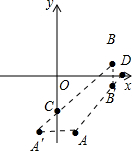
| 6 |
| 7 |
| 23 |
| 7 |
| 23 |
| 7 |
| 23 |
| 7 |
| 4 |
| 3 |
| 23 |
| 3 |
| 23 |
| 4 |
| 23 |
| 4 |


科目:初中数学 来源: 题型:
 如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=5
如图,矩形ABCD中,E为CD的中点,连接AE并延长交BC的延长线于点F,连接BD交AF于H,AD=5| 2 |
| ||
| 4 |
A、
| ||||
B、5
| ||||
| C、10 | ||||
| D、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 每台购入价(万元) | 每台每天可淡化海水量(立方米) | 淡化率 | |
| A型 | 20 | 250 | 80% |
| B型 | 25 | 400 | 75% |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,菱形ABCD中,点M为AD的中点,点N在AB上,DE⊥BC的延长线于点E,连接BM、DN、EN,∠AND=∠MBC.
如图,菱形ABCD中,点M为AD的中点,点N在AB上,DE⊥BC的延长线于点E,连接BM、DN、EN,∠AND=∠MBC.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
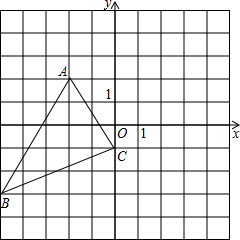 如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com