
已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
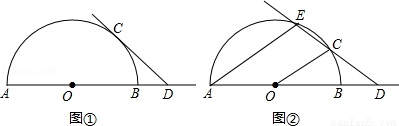
(1) ∠ODC=45°;(2) AE=OD.理由见解析;∠ODC=36°.
【解析】
试题分析:(1)连接OC,因为CD是⊙O的切线,得出∠OCD=90°,由OC=CD,得出∠ODC=∠COD,即可求得.
(2)连接OE,
①证明△AOE≌△OCD,即可得AE=OD;
②利用等腰三角形及平行线的性质,可求得∠ODC的度数.
试题解析:(1)如图①,连接OC,
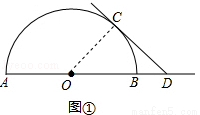
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
(2)如图②,连接OE.
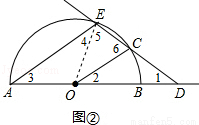
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°-2x.
①AE=OD.理由如下:
在△AOE与△OCD中,

∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°.
【考点】直线与圆的位置关系;平行线的性质;全等三角形的判定与性质.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源:2014年初中毕业升学考试(贵州六盘水卷)数学(解析版) 题型:填空题
如图,在△ABC中,∠A=90°,AB=6,AC=8,分别以点B和C为圆心的两个等圆外切,则图中阴影部分面积为 (结果保留π)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建南平卷)数学(解析版) 题型:选择题
如图,将1、 、
、 三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(2014,2014)表示的两个数的积是( )
三个数按图中方式排列,若规定(a,b)表示第a排第b列的数,则(8,2)与(2014,2014)表示的两个数的积是( )

A. B.
B. C.
C. D.1
D.1
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建南平卷)数学(解析版) 题型:选择题
一个袋中只装有3个红球,从中随机摸出一个是红球( )
A.可能性为 B.属于不可能事件 C.属于随机事件 D.属于必然事件
B.属于不可能事件 C.属于随机事件 D.属于必然事件
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃天水卷)数学(解析版) 题型:解答题
空气质量的优劣直接影响着人们的身体健康.天水市某校兴趣小组,于2014年5月某一周,对天水市区的空气质量指数(AQI)进行监测,监测结果如图.请你回答下列问题:
(1)这一周空气质量指数的极差、众数分别是多少?
(2)当0≤AQI≤50时,空气质量为优.这一周空气质量为优的频率是多少?
(3)根据以上信息,谈谈你对天水市区空气质量的看法.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:选择题
下列命题中正确的是( )
A.有一组邻边相等的四边形是菱形
B.有一个角是直角的平行四边形是矩形
C.对角线垂直的平行四边形是正方形
D.一组对边平行的四边形是平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com