
分析 根据解无理方程的方法可以解答题目中的方程,从而可以解答本题.
解答 解:∵4$\sqrt{\frac{1}{8}}$-$\sqrt{3x}$=$\sqrt{32}$
∴$\sqrt{\frac{16}{4}}-\sqrt{3x}=4\sqrt{2}$
∴2-$\sqrt{3x}=4\sqrt{2}$
∴2-4$\sqrt{2}$=$\sqrt{3x}$
∴3x=(2-4$\sqrt{2}$)2
∴x=$\frac{(2-4\sqrt{2})^{2}}{3}$
∴x=$\frac{36-16\sqrt{2}}{3}$.
点评 本题考查无理方程,解答本题的关键是明确无理方程的解答方法,注意方程中是$\sqrt{3x}$,不要误认为是$\sqrt{3}x$.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有解,x=1 | B. | 有解,x=5 | C. | 有解,x=4 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
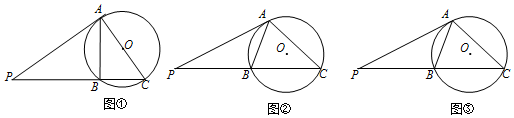
 已知,矩形ABCD中,AB=10,AD=25,P、Q分别是AB、CD的中点,点O从P点出发,以每秒一个单位的速度,沿着PQ向Q点移动,移动时间为t秒,当到达Q点时停止运动,在运动过程中,以O为圆心,OA长为半径的⊙O与矩形四边的交点个数会出现哪些情况?请直接写出,并指明对应的t的取值范围.
已知,矩形ABCD中,AB=10,AD=25,P、Q分别是AB、CD的中点,点O从P点出发,以每秒一个单位的速度,沿着PQ向Q点移动,移动时间为t秒,当到达Q点时停止运动,在运动过程中,以O为圆心,OA长为半径的⊙O与矩形四边的交点个数会出现哪些情况?请直接写出,并指明对应的t的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
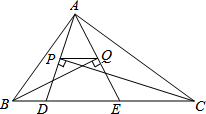 如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )
如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )| A. | 8 | B. | 6 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
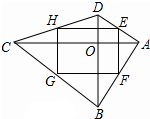 在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )| A. | AC平分BD | B. | AC⊥BD | C. | AC=BD | D. | AC与BD互相平分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com