

分析 (1)根据tan∠C1OB1=$\frac{{B}_{1}{C}_{1}}{O{C}_{1}}$=$\frac{\sqrt{3}}{3}$,求出∠C1OB1=30°,由此即可解决问题.
(2)如图2中,结论::①DE+DF是定值.只要证明△OFD≌△OEB1(AAS),推出DF=EB1、DE+DF=DE+EB1=DB1=2$\sqrt{2}$为定值.
(3)如图3中,取OP的中点N,连接MN、HN、AH.只要证明△MNH≌△AOH(SAS),推出HM=HA,∠MHN=∠AHO,由∠MHN+∠MHO=60°,推出∠AHO+∠MHO=60°,推出△MAH为等边三角形,由此即可解决问题.
解答 解:(1)如图1中,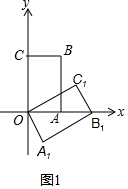
∵OC1=OC=$\sqrt{3}$,B1C1=OA=1,
∴tan∠C1OB1=$\frac{{B}_{1}{C}_{1}}{O{C}_{1}}$=$\frac{\sqrt{3}}{3}$,
∴∠C1OB1=30°,
∴C1($\frac{3}{2},\frac{\sqrt{3}}{2}$).
(2)如图2中,结论::①DE+DF是定值.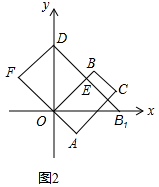
理由:∵OB=OB1=2,
∴OB1=OD,
∴△OB1D为等腰直角三角形
∵∠FDB1=90°,
∴∠FDO=45°,
∵∠AOB=90°,
∴∠FOB=90°,
在四边形FOED中,∠OFD+∠OED=180°
∵∠OED+∠OEB1=180°,
∴∠OFD=∠OEB1,
∴△OFD≌△OEB1(AAS),
∴DF=EB1,
∴DE+DF=DE+EB1=DB1=2$\sqrt{2}$为定值.
(3)如图3中,取OP的中点N,连接MN、HN、AH.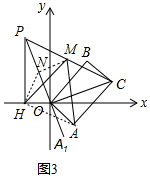
∵PH⊥x轴,
∴HN=MN,
由(1)得,∠A1Ox=60°=∠POH,
∴△HON为等边三角形,
∴OH=HN,
∵M为PC的中点,
∴MN=$\frac{1}{2}$OC=OA,设∠MNO=α,则∠POC=180°-α
∴∠MNH=60°+α
∵∠HOA=360°-60°-60°-(180°-α)=60°+α
∴∠HOA=∠MNH,
∴△MNH≌△AOH(SAS),
∴HM=HA,∠MHN=∠AHO,
∵∠MHN+∠MHO=60°,
∴∠AHO+∠MHO=60°,
∴△MAH为等边三角形,
∴∠AMH=60°为定值.
点评 本题考查四边形综合题、矩形的性质、等腰直角三角形的性质、全等三角形的判定和性质,等边三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
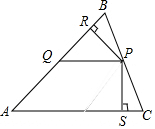 如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR②AQ=PQ③△PQR≌△CPS,其中正确的是( )
如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR②AQ=PQ③△PQR≌△CPS,其中正确的是( )| A. | ①③ | B. | ①② | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5<$\sqrt{11}$<3 | B. | $\sqrt{11}$<3.5<3 | C. | 3<$\sqrt{11}$<3.5 | D. | 3<3.5<$\sqrt{11}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽. 如果设小路宽为x,根据题意,所列方程正确的是( )
如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为540m2,求道路的宽. 如果设小路宽为x,根据题意,所列方程正确的是( )| A. | (32+x)(20+x)=540 | B. | (32-x)(20-x)=540 | C. | (32+x)(20-x)=540 | D. | (32-x)(20+x)=54 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
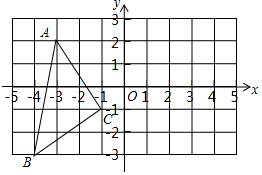 如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
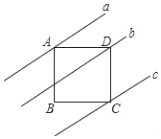 如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是4,b与c之间的距离是8,则正方形ABCD的面积是( )
如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是4,b与c之间的距离是8,则正方形ABCD的面积是( )| A. | 70 | B. | 74 | C. | 80 | D. | 144 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com