
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),直线y=kx﹣3经过B、C两点.
(1)求k的值既抛物线的函数表达式;
(2)如果P是线段BC上一点,设△ABP、△APC的面积分别为S△ABP、S△APC,且S△ABP:S△APC=2:3,求点P的坐标;
(3)设⊙Q的半径为1,圆心Q在抛物线上运动,则在运动过程中是否存在⊙O与坐标轴相切的情况?若存在,求出圆心Q的坐标;若不存在,请说明理由,并探究:若设⊙Q的半径为r,圆心Q在抛物线上运动,则当r取何值时,⊙Q与两坐标轴同时相切?
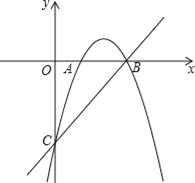
【答案】(1)y=﹣x2+4x﹣3;(2)P点的纵坐标为(![]() ,﹣
,﹣![]() );(3)①Q点的坐标为(﹣1,8);
);(3)①Q点的坐标为(﹣1,8);
②存在⊙Q与坐标轴相切,圆心Q的坐标为(1,0),(﹣1,8),(2+![]() ,﹣1),(2﹣
,﹣1),(2﹣![]() ,﹣1);
,﹣1);
③当r=![]() 时,⊙Q与两坐标轴同时相切.
时,⊙Q与两坐标轴同时相切.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据面积的比,可得PB∶PC的值,根据相似三角形的判定与性质,可得PD的长,根据自变量与函数值的对应关系,可得答案;
(3)根据圆与坐标轴相切,可得x或y的值,再根据自变量与函数值的对应关系,可得Q点坐标.
(1)将B点坐标代入y=kx﹣3,得3k﹣3=0,解得k=1;
直线的解析式为y=x﹣3,当x=0时,y=﹣3,即C点坐标为(0,﹣3),
将B、C点坐标代入抛物线的解析式,解得b=4,c=﹣3,
抛物线的解析式为y=﹣x2+4x﹣3;
(2)作PD⊥AB于D点,如图:

由S△ABP:S△APC=2:3,得PB:PC=2:3,PB:BC=2:5.
由△PBD∽△COB,得![]() =
=![]() ,解得DP=
,解得DP=![]() ,
,
解得P点的纵坐标为﹣![]() ,当y=﹣
,当y=﹣![]() 时,x﹣3=﹣
时,x﹣3=﹣![]() ,解得x=
,解得x=![]() ,
,
得P点的纵坐标为(![]() ,﹣
,﹣![]() );
);
(3)设Q(x,y),
①当⊙Q与y轴相切时,有|x|=1,即x=±1.
当x=1时,y=﹣x2+4x﹣3=0,即Q点的坐标为(1,0),
当x=﹣1时,y=﹣x2+4x﹣3=﹣8,得Q点的坐标为(﹣1,8);
②当⊙Q与x轴相切时,有|y|=1,即y=±1.
当y=1时,1=﹣x2+4x﹣3,解得x=2,即Q点的坐标为(2,1);
当y=﹣1时,﹣1=﹣x2+4x﹣3,解得x=2![]() ,即Q(2+
,即Q(2+![]() ,﹣1),(2﹣
,﹣1),(2﹣![]() ,﹣1),
,﹣1),
综上所述:存在⊙Q与坐标轴相切,圆心Q的坐标为(1,0),(﹣1,8),(2+![]() ,﹣1),(2﹣
,﹣1),(2﹣![]() ,﹣1);
,﹣1);
③当⊙Q与两坐标轴同时相切时,有|x|=|y|.
当y=x时,﹣x2+4x﹣3=x,此方程无解;
当y=﹣x时,﹣x2+4x﹣3=﹣x,解得x=![]() ,当r=
,当r=![]() 时,⊙Q与两坐标轴同时相切,
时,⊙Q与两坐标轴同时相切,
综上所述:当r=![]() 时,⊙Q与两坐标轴同时相切.
时,⊙Q与两坐标轴同时相切.


科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形中,点A,B,C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′
(2)三角形ABC的面积为 ;
(3)在直线l上找一点P,使PA+PB的长最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
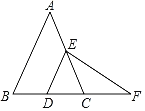
【题目】如图,在△ABC中,AB=AC,DE∥AB,分别交BC、AC于点D、E,点F在BC的延长线上,且CF=DE.
(1)求证:△CEF是等腰三角形;
(2)连接AD,当AD⊥BC,BC=8,△CEF的周长为16时,求△DEF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠BAC=90°,AB=AC,∠ADB=45°

(1)求证:BD⊥CD;
(2)若BD=6,CD=2,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与正比例函数
的图像与正比例函数![]() 的图像都经过点
的图像都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 在正比例函数
在正比例函数![]() 的图像上.
的图像上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一点)的路线是抛物线![]() 的一部分,如图
的一部分,如图

(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“快乐分式”.如:![]() ,则
,则 ![]() 是“快乐分式”.
是“快乐分式”.
(1)下列式子中,属于“快乐分式”的是 (填序号);
①![]() ,②
,② ![]() ,③
,③![]() ,④
,④ ![]() .
.
(2)将“快乐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() = .
= .
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明听说“武黄城际列车”已经开通,便设计了如下问题:如图,以往从黄石A坐客车到武昌客运站B,现在可以在黄石A坐“武黄城际列车”到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80 km,BC=20 km,∠ABC=120°.请你帮助小明解决以下问题:
(1)求A,C之间的距离.(参考数据![]() ≈4.6)
≈4.6)
(2)若客车的平均速度是60 km/h,市内的公共汽车的平均速度为40 km/h,“武黄城际列车”的平均速度为180 km/h,为了在最短时间内到达武昌客运站,小明应选择哪种乘车方案?请说明理由.(不计候车时间)
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com