
【题目】如图1,△ABC为等腰直角三角形,∠ACB=90,F是AC边上的一个动点(点F与A. C不重合),以CF为一边在等腰直角三角形外作正方形CDEF,连接BF、AD.
(1)猜想图1中线段BF、AD的数量关系及所在直线的位置关系,直接写出结论;
(2)将图1中的正方形CDEF,绕着点C按顺时针方向旋转任意角度α,得到如图2的情形。图2中BF交AC于点H,交AD于点O,请你判断(1)中得到的结论是否仍然成立,并证明你的判断。
(3)将原题中的等腰直角三角形ABC改为直角三角形ABC,∠ACB=90,正方形CDEF改为矩形CDEF,如图3,且AC=4,BC=3,CD=![]() ,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。
,CF=1,BF交AC于点H,交AD于点O,连接BD、AF,求BD2+AF2的值。

【答案】(1) BF=AD,BF⊥AD;(2) BF=AD,BF⊥AD仍然成立,理由见解析;(3)![]() .
.
【解析】分析:(1)可由SAS证得△BCF≌△ACD得到BF=AD,BF⊥AD;(2)与(1)中的方法相同;(3)证△BCF∽△ACD,得BO⊥AD,再利用勾股定理求解.
详解:(1)BF=AD,BF⊥AD;
(2)BF=AD,BF⊥AD仍然成立,
证明:∵△ABC是等腰直角三角形,∠ACB=90,∴AC=BC,
∵四边形CDEF是正方形,∴CD=CF,∠FCD=90,
∴∠ACB+∠ACF=∠FCD+∠ACF,即∠BCF=∠ACD,
在△BCF和△ACD中
BC=AC,∠BCF=∠ACD,CF=CD,
∴△BCF≌△ACD(SAS),∴BF=AD,∠CBF=∠CAD,
又∵∠BHC=∠AHO,∠CBH+∠BHC=90,
∴∠CAD+∠AHO=90,∴∠AOH=90,
∴BF⊥AD;
(3)证明:连接DF,

∵四边形CDEF是矩形,∴∠FCD=90,
又∵∠ACB=90,∴∠ACB=∠FCD
∴∠ACB+∠ACF=∠FCD+∠ACF,即∠BCF=∠ACD,
∵AC=4,BC=3,CD=![]() ,CF=1,∴BC:AC=CF:CD=3:4,
,CF=1,∴BC:AC=CF:CD=3:4,
∴△BCF∽△ACD,∴∠CBF=∠CAD,
又∵∠BHC=∠AHO,∠CBH+∠BHC=90
∴∠CAD+∠AHO=90,∴∠AOH=90,∴BF⊥AD,
∴∠BOD=∠AOB=90,
∴BD2=OB2+OD2,AF2=OA2+OF2,AB2=OA2+OB2,DF2=OF2+OD2,
∴BD2+AF2=OB2+OD2+OA2+OF2=AB2+DF2,
∵在Rt△ABC中,∠ACB=90,AC=4,BC=3,
∴AB2=AC2+BC2=32+42=25,
∵在Rt△FCD中,∠FCD=90,CD=![]() ,CF=1,
,CF=1,
∴DF2=CD2+CF2=(![]() )2+12=
)2+12=![]() ,
,
∴BD2+AF2=AB2+DF2=25+![]() .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A地在数轴上表示的数为-16,AB两地相距50个单位长度.小明从A地出发去B地,以每分钟2个单位长度的速度行进,第一次他向左1单位长度,第二次向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度…,按此规律行进.
![]()
(1)求出B地在数轴上表示的数;
(2)若B地在原点的右侧,经过第8次行进后小明到达点P,此时点P与点B相距几个单位长度?8次运动完成后一共经过了几分钟?
(3)若经过n次(n为正整数)行进后,小明到达点Q,请你直接写出:点Q在数轴上表示的数应如何表示?
查看答案和解析>>
科目:初中数学 来源: 题型:
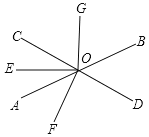
【题目】如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,CD⊥AB于点D,BD=9,BC=15,AC=20.
(1)求CD的长;
(2)求AB的长;
(3)判断△ABC的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受到中学生的喜爱,各种品牌相继投放市场,某车行经营的A型车去年销售总额为5万元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
A,B两种型号车的进货和销售价格如下表:
A型车 | B型车 | |
进货价格(元) | 1 100 | 1 400 |
销售价格(元) | 今年的销售价格 | 2 000 |
(1)今年A型车每辆售价多少元?(用列方程的方法解答)
(2)该车行计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个电子厂在广告中都声称他们的某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查,统计结果如下:(单位:年)
甲厂:3,4,5,6,7 乙厂:4,4,5,6,6
(1)分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差;
(2)如果你是顾客,你会选购哪家电子厂的产品?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.
收集数据:随机抽取甲乙两所学校的20名学生的数学成绩进行分析:
甲 | 91 | 89 | 77 | 86 | 71 | 31 | 97 | 93 | 72 | 91 |
81 | 92 | 85 | 85 | 95 | 88 | 88 | 90 | 44 | 91 | |
乙 | 84 | 93 | 66 | 69 | 76 | 87 | 77 | 82 | 85 | 88 |
90 | 88 | 67 | 88 | 91 | 96 | 68 | 97 | 59 | 88 |
整理、描述数据:按如下数据段整理、描述这两组数据
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
|
|
|
|
|
|
|
分析数据:两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | m | 115.25 |
经统计,表格中m的值是 .
得出结论:
a若甲学校有400名初二学生,估计这次考试成绩80分以上人数为 .
b可以推断出 学校学生的数学水平较高,理由为 .(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com