
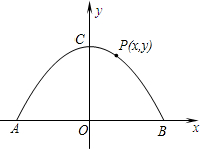
 如图,二次函数y=-
如图,二次函数y=-| 1 |
| 2 |
科目:初中数学 来源: 题型:
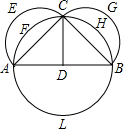 如图,分别以等腰Rt△ABC的边AC、BC为直径画半圆,以边AB为直径画圆.则:
如图,分别以等腰Rt△ABC的边AC、BC为直径画半圆,以边AB为直径画圆.则:| 1 |
| 2 |
| A、①②③ | B、①④ |
| C、②③④ | D、①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
|
|
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 组别 | 垫球个数x(个) | 频数(人数) | 频率 |
| 1 | 10≤x<20 | 5 | 0.10 |
| 2 | 20≤x<30 | a | 0.18 |
| 3 | 30≤x<40 | 20 | b |
| 4 | 40≤x<50 | 16 | 0.32 |
| 合计 | 1.00 |
| 排球30秒对墙垫球的中考评分标准 | ||||||||||
| 分值 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 排球(个) | 40 | 36 | 33 | 30 | 27 | 23 | 19 | 15 | 11 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
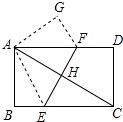 如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com