
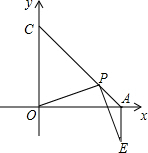
 已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.
已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由. 分析 作OG⊥AC,EF⊥AC,垂足分别为G、F,首先利用等腰直角三角AOC,得出条件证得△OGP≌△PFE,OG=PF=AG,GP=EF,进一步证得△AEF是等腰直角三角形得出结论AE⊥OA即可.
解答 AE⊥OA.
证明:如图,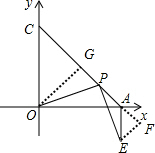
作OG⊥AC,EF⊥AC,垂足分别为G、F,
∵∠AC0=45°,∠A0C=90°,
∴∠OAC=∠OCA=45°,
∴OA=OC,
∴OG=CG=AG,
∵PE⊥OP,
∴∠OPG+∠EPF=∠GOP+∠OPG=90°,
∴∠GOP=∠EPF,
在△OGP和△PFE中,
$\left\{\begin{array}{l}{∠GOP=∠FPE}\\{∠OGP=∠EFP}\\{OP=PE}\end{array}\right.$,
∴△OGP≌△PFE,
∴OG=PF=AG,GP=EF,
∴AG-AP=PF-AP,
∴GP=AF=EF,
∴∠EAF=45°,
∴AOE=90°,
∴AE⊥OA.
点评 此题考查三角形全等的判定与性质,等腰直角三角形的性质,正确作出辅助线,构造出全等的三角形是解决问题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:解答题
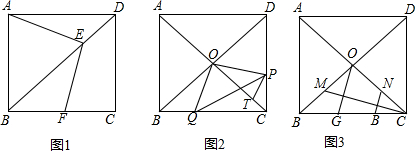
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
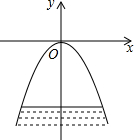 如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.
如图,拱桥的形状是抛物线,其函数关系式为y=$\frac{1}{3}$x2,当水面离桥顶的高度为$\frac{25}{3}$米时,水面的宽度为10米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
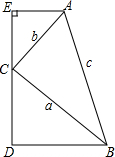 如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.
如图,在四边形ABDE中,∠E=90°,AE∥BD,C为ED上一点,设△ABC三边分别为a、b、c,且方程(a+c)x2-2bx-a+c=0有两相等实根.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
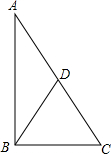 如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.
如图,已知Rt△ABC中,∠ABC=90°,△ABC的周长为17cm,斜边上中线BD长为$\frac{7}{2}$cm.则该三角形的面积为$\frac{51}{4}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com