
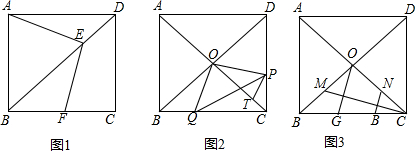
分析 (1)过点E作MN⊥BC,则MN⊥AD,证明△AME≌△ENF,得到FN=EM=$\frac{\sqrt{2}}{2}$DE,根据图形计算即可;
(2)作TM⊥BC于M,TH⊥DC于H,TN⊥QP于N,根据角平分线的性质得到TM=TH=TN=$\frac{\sqrt{2}}{2}$TC,证明△OBQ≌△OCP,得到BQ=CP,得到答案;
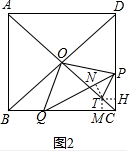
(3)作BP⊥BD交OG的延长线于P,交NB的延长线于R,证明四边形OPRN是平行四边形和△COM≌△OBP,求出答案.
解答 (1)证明: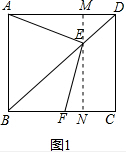 过点E作MN⊥BC,则MN⊥AD,
过点E作MN⊥BC,则MN⊥AD,
则△DME是等腰直角三角形,
∴DM=EM=$\frac{\sqrt{2}}{2}$DE,
∵AE⊥EF,
∴∠AEF=90°,
∴∠AEM+∠FEN=90°,又∠EFN+∠FEN=90°,
∴∠EFN=∠AEM,又EN=BN=AM,
在△AME和△ENF中,
$\left\{\begin{array}{l}{∠AEM=∠EFN}\\{AM=EN}\\{∠AME=∠ENF}\end{array}\right.$,
∴△AME≌△ENF,
∴FN=EM=$\frac{\sqrt{2}}{2}$DE,
∴AB-BF=BC-BF=FN+NC=$\frac{\sqrt{2}}{2}$DE+$\frac{\sqrt{2}}{2}$DE=$\sqrt{2}$ED;
(2) 证明:作TM⊥BC于M,TH⊥DC于H,TN⊥QP于N,
证明:作TM⊥BC于M,TH⊥DC于H,TN⊥QP于N,
∵PT是∠QPC的角平分线,OC是∠DCB的角平分线,
∴TM=TH=TN=$\frac{\sqrt{2}}{2}$TC,
在△OBQ和△OCP中,
$\left\{\begin{array}{l}{∠BOQ=∠COP}\\{OB=OC}\\{∠OBQ=∠OCP}\end{array}\right.$,
∴△OBQ≌△OCP
∴BQ=CP,
BC-QP=BQ+QM+MC-(QN+NP)=TM+TH=$\frac{\sqrt{2}}{2}$TC+$\frac{\sqrt{2}}{2}$TC=$\sqrt{2}$TC;
(3) 解:作BP⊥BD交OG的延长线于P,交NB的延长线于R,
解:作BP⊥BD交OG的延长线于P,交NB的延长线于R,
∵四边形ABCD是正方形,
∴∠BOC=90°,
∴OC∥BR,又OG∥BN,
∴四边形OPRN是平行四边形,
∴ON=PR,
由(1)得,△COM≌△OBP,
∴OM=BP,
∵BG=$\frac{4}{5}GH$,又∵OG∥BN,
∴$\frac{BP}{PR}$=$\frac{4}{5}$,即$\frac{OM}{ON}$=$\frac{4}{5}$.
点评 本题考查的是正方形的性质、相似三角形的判定定理和性质定理,正确作出辅助线、灵活运用相似三角形的判定定理和性质定理是解题的关键.


科目:初中数学 来源: 题型:解答题
 测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题
测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
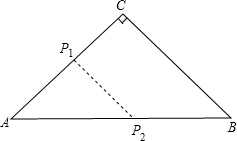 如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )
如图所示,△ABC为等腰直角三角形,P1,P2分别从A,B出发,速度都是1cm/s,P1运动到C为止,AB=100cm,t(s)后,S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t(s)的函数关系为( )| A. | S=t(100-t) | B. | S=$\frac{\sqrt{2}}{2}{t}^{2}-5\sqrt{2}t$ | C. | S=$\frac{\sqrt{2}}{2}{t}^{2}$ | D. | S=-$\frac{\sqrt{2}}{4}{t}^{2}+25\sqrt{2}t$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 △ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )
△ABC中,AB=AC=12厘米,∠B=∠C,BC=9厘米,点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为( )| A. | 2.5 | B. | 3 | C. | 2.25或3 | D. | 1或5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
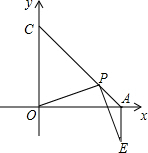 已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.
已知∠AC0=45°,P是线段AC上任一点,(P不与A、C重合),连OP,作PE⊥OP,且PE=OP,连AE,试判断AE和OA的位置关系,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com