
科目:初中数学 来源: 题型:解答题
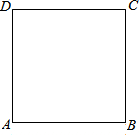 如图,四边形ABCD为正方形,利用尺规作图在正方形ABCD内(含边),画出使∠APB=60°的所有的点构成的图形.(要求:不写作法,保留作图痕迹,写出结论)
如图,四边形ABCD为正方形,利用尺规作图在正方形ABCD内(含边),画出使∠APB=60°的所有的点构成的图形.(要求:不写作法,保留作图痕迹,写出结论)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
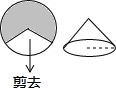 如图,如果将半径为10cm的圆形纸片剪去一个圆心角为120°的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为$\frac{20}{3}$cm.
如图,如果将半径为10cm的圆形纸片剪去一个圆心角为120°的扇形,用剩下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的底面圆半径为$\frac{20}{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
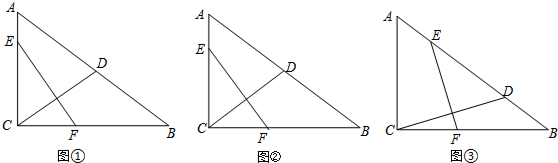
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
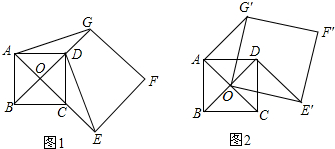
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com