Question

小王玩游戏，一张纸片，第一次将其撕成四小片，以后每次都将其中一片撕成更小的四片，如此进行下去，当小王撕到第n次时，手中共有s张纸片．
（1）当小王撕了3次时，他手中有几张纸？
（2）用含有n的代数式表示s，并求小王要得到82张纸片需撕多少次？
（3）小王说：“我撕了若干次后，手中的纸片有2009张”，小王说的对不对？若不对，请说出你的理由；若对的，请指出小王需撕多少次？

Answer 1

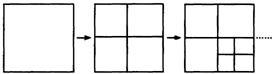
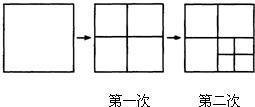
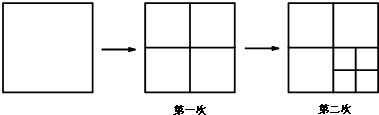
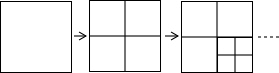
解：（1）从图中可以看出，当小王撕了1次时，手中有4张纸=3×1+1；
当小王撕了2次时，手中有7张纸=3×2+1；
…
可以发现：小王撕了几次后，他手中纸的张数等于3与几的乘积加1．
所以，当小王撕了3次时，手中有3×3+1=10张纸．
答：当小王撕了3次时，手中有10张纸；

（2）设撕的次数为n，纸的张数为s，按照（1）中的规律可得：s=3n+1．
当s=82时，3n+1=82，n=27．
答：代数式为s=3n+1；小王要得到82张纸片需撕27次；

（3）将2009代入s=3n+1中可得：n=，
∵这个数不是整数，
∴小王说的不对．
分析：（1）分别数出三个图形中正方形的个数，第二个和第三个图形中正方形的个数就是小王分别撕了一次和两次后手中纸的张数．就是小王可以发现小王撕了几次后，他手中纸的张数等于3与几的乘积加1．如当小王撕了2次时，手中有7张纸=3×2+1；由此可得，小王撕了3次时，手中有3×3+1=10张纸．
（2）设撕的次数为n，纸的张数为s，按照（1）中的规律即可得出答案，将s=82代入代数式，即可求得撕纸的次数．
（3）将2009代入代数式，如果得数为整数，则说明小王说的对；如果得数不是整数，则说明小王说的不对．
点评：此题主要考查学生对图形变化类这个知识点的理解和掌握，解答此类题目的关键是根据题目中给出的图形，数值等条件，认真分析，找到规律．此类题目难度一般偏大，属于难题．