Question

【题目】在“学本课堂”的实践中，王老师经常让学生以“问题”为中心进行自主、合作、探究学习.

（课堂提问）王老师在课堂中提出这样的问题：如图1，在Rt△ABC中，∠ACB=90°，∠BAC=30°，那么BC和AB有怎样的数量关系？

（互动生成）经小组合作交流后，各小组派代表发言.

（1）小华代表第3小组发言：AB=2BC. 请你补全小华的证明过程.

证明：把△ABC沿着AC翻折，得到△ADC.

∴∠ACD=∠ACB=90°，

∴∠BCD=∠ACD+∠ACB=90°+90°=180°，

即：点B、C、D共线.

（请在下面补全小华的证明过程）

（2）受到第3小组“翻折”的启发，小明代表第2小组发言：如图2，在△ABC中，如果把条件“∠ACB=90°”改为“∠ACB=135°”，保持“∠BAC=30°”不变，若BC=1，求AB的长.

（能力迁移）我们发现，翻折可以探索图形性质，请利用翻折解决下面问题.

如图3，点D是△ABC内一点，AD=AC，∠BAD=∠CAD=20°，∠ADB+∠ACB=210°，则AD、DB、BC三者之间的数量关系是 .

（课后拓展）如图4，在四边形ABCD中，∠BCD=45°，∠BAD=90°，∠ADB=∠CDB=60°，且AC=1，

则△ABD的周长为 .

Answer 1

【答案】(1)见解析；（2）；能力迁移：；课后拓展：.

【解析】

（1）根据提示证明出△ABD为等边三角形即可说明BC和AB的关系；

（2）过点B作AC边的垂线，交AC的延长线于点D，设BD=x，则CD=BC=x，解出x即可；

能力迁移：把△ABD延AB边翻折得到△AEB，连接ED，EC，先通过角度转换得到∠EBC=90°，在证明BC=BD，EC=AD，即可求出AD、DB、BC三边的关系；

课后拓展：作BD⊥CD于点E，作CF垂直AD的延长线于点F，设AD=x，BD=2AD=2x，然后表示出AF，CF边建立方程解出x即可.

（1）证明：把△ABC沿着AC翻折，得到△ADC.

∴∠ACD=∠ACB=90°，

∴∠BCD=∠ACD+∠ACB=90°+90°=180°，

即：点B、C、D共线，

∴AB=AD，

∵∠BAC=30°，

∴∠ABC=60°，

∴△ABD为等边三角形，

∴AB=BD=2BC；

（2）过点B作AC边的垂线，交AC的延长线于点D，

∵∠ACB=135°，

∴∠BCD=45°，

∵∠BDC=90°，BC=1，

设BD=x，则CD=BC=x，

∴，解得：，

∵∠BAC=30°，

∴AB=2BD=；

能力迁移：

把△ABD延AB边翻折得到△AEB，连接ED，EC，

∵∠BAD=∠CAD=20°，

∴∠EAB=20°，

∴∠EAC=60°，

∵∠ACB+∠ADB=210°，∠AEB=∠ADB，

∴∠ACB=∠AEB=210°，

∴∠EBC=360°-210°-60°=90°，

∵AD=AC，AE=AD，

∴AE=AC，

∴△AEC为等边三角形，

∴EC=AE=AD，

在Rt△EBC中，，

∵BC=BD，EC=AD，

∴；

课后拓展：

作BD⊥CD于点E，作CF垂直AD的延长线于点F，

∵∠BAD=90°，∠ADB=∠CDB=60°，

∴△BAD≌△BED，

∵∠BCD=45°，

∴BE=CE，

设AD=x，

∴BD=2AD=2x，

∴，

∴EC=EB=AB=，

∴DC=，

∴∠FDC=60°，∠ECD=30°，

∴DF=，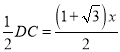

∴，

,

∵AC=1，

在Rt△AFC中，，

则，解得：，

AD=，

DB=，

则△ABD的周长为：.