练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如图，直线a∥b，∠1=75°，∠2=35°，则∠3的度数是（　　）
    A．75°B．55°C．40°D．35°

    分析 根据平行线的性质得出∠4=∠1=75°，然后根据三角形外角的性质即可求得∠3的度数．

    解答 解：∵直线a∥b，∠1=75°，
    ∴∠4=∠1=75°，
    ∵∠2+∠3=∠4，
    ∴∠3=∠4-∠2=75°-35°=40°．
    故选C．

    点评 本题考查了平行线的性质和三角形外角的性质，熟练掌握性质定理是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

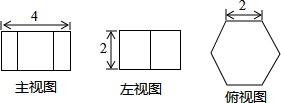    7．如图是某几何体的三视图，则该几何体的表面积为（　　）
    A．16+6$\sqrt{3}$B．16+12$\sqrt{3}$C．24+6$\sqrt{3}$D．24+12$\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

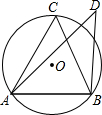    8．如图，若锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），则下列三个结论：①sin∠C＞sin∠D；②cos∠C＞cos∠D；③tan∠C＞tan∠D中，正确的结论为（　　）
    A．①②B．②③C．①②③D．①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列几何体的主视图与其他三个不同的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于$\frac{1}{2}$GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．
    （1）求证：AB=AE；
    （2）若∠A=100°，求∠EBC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=5$\sqrt{5}$，且$\frac{OD}{OE}$=$\frac{4}{3}$，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y=-$\frac{1}{16}$x2+$\frac{1}{2}$x+c经过点E，且与AB边相交于点F．
    （1）求证：△ABD∽△ODE；
    （2）若M是BE的中点，连接MF，求证：MF⊥BD；
    （3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．阳泉同学参加周末社会实践活动，到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数：
    32 39 45 55 60 54 60 28 56 41
    51 36 44 46 40 53 37 47 45 46
    （1）前10株西红柿秧上小西红柿个数的平均数是47，中位数是49.5，众数是60；
    （2）若对这20个数按组距为8进行分组，请补全频数分布表及频数分布直方图
    个数分组28≤x＜3636≤x＜4444≤x＜5252≤x＜6060≤x＜68
    频数25742
    （3）通过频数分布直方图试分析此大棚中西红柿的长势．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．甲、乙两布袋装有红、白两种小球，两袋装球总数量相同，两种小球仅颜色不同．甲袋中，红球个数是白球个数的2倍；乙袋中，红球个数是白球个数的3倍，将乙袋中的球全部倒入甲袋，随机从甲袋中摸出一个球，摸出红球的概率是（　　）
    A．$\frac{5}{12}$B．$\frac{7}{12}$C．$\frac{17}{24}$D．$\frac{2}{5}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列运算错误的是（　　）
    A．$（\frac{1}{2}）^{0}$=1B．x2+x2=2x4C．|a|=|-a|D．$（\frac{b}{{a}^{2}}）^{3}$=$\frac{{b}^{3}}{{a}^{6}}$

    查看答案和解析>>

    同步练习册答案