
【题目】综合与探究
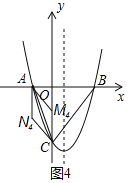
如图,抛物线y=x2+bx+c与x轴交于A、B两点,与y轴交于C点,OA=2,OC=6,连接AC和BC.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,当△ACD的周长最小时,点D的坐标为 .
(3)点E是第四象限内抛物线上的动点,连接CE和BE.求△BCE面积的最大值及此时点E的坐标;
(4)若点M是y轴上的动点,在坐标平面内是否存在点N,使以点A、C、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣x﹣6;(2)(![]() ,﹣5);(3)点E坐标为(
,﹣5);(3)点E坐标为(![]() ,﹣
,﹣![]() )时,△BCE面积最大,最大值为
)时,△BCE面积最大,最大值为![]() ;(4)存在点N,点N坐标为(﹣2,2
;(4)存在点N,点N坐标为(﹣2,2![]() ),(﹣2,﹣2
),(﹣2,﹣2![]() ),(2,0),(﹣2,﹣
),(2,0),(﹣2,﹣![]() ).
).
【解析】
(1)用待定系数法求解;
(2)当点B、D、C在同一直线上时,C△ACD=AC+AD+CD=AC+BD+CD=AC+BC最小;求出直线BC:y=2x﹣6,可进一步求解;
(3)过点E作EG⊥x轴于点G,交直线BC与点F,设E(t,t2﹣t﹣6)(0<t<3),则F(t,2t﹣6),得EF=2t﹣6﹣(t2﹣t﹣6)=﹣t2+3t,S△BCE=S△BEF+S△CEF=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,可得结果;
,可得结果;
(4)存在点N,使以点A、C、M、N为顶点的四边形是菱形.可分情况若AC为菱形的边长,MN∥AC且,MN=AC=2![]() ;若AC为菱形的对角线,则AN4∥CM4,AN4=CN4,N4(﹣2,n),由勾股定理可求n.
;若AC为菱形的对角线,则AN4∥CM4,AN4=CN4,N4(﹣2,n),由勾股定理可求n.
(1)∵OA=2,OC=6
∴A(﹣2,0),C(0,﹣6)
∵抛物线y=x2+bx+c过点A、C
∴![]()
解得:![]()
∴抛物线解析式为y=x2﹣x﹣6
(2)∵当y=0时,x2﹣x﹣6=0,解得:x1=﹣2,x2=3
∴B(3,0),抛物线对称轴为直线x=![]()
∵点D在直线x=![]() 上,点A、B关于直线x=
上,点A、B关于直线x=![]() 对称
对称
∴xD=![]() ,AD=BD
,AD=BD
∴当点B、D、C在同一直线上时,C△ACD=AC+AD+CD=AC+BD+CD=AC+BC最小
设直线BC解析式为y=kx﹣6
∴3k﹣6=0,解得:k=2
∴直线BC:y=2x﹣6
∴yD=2×![]() ﹣6=﹣5
﹣6=﹣5
∴D(![]() ,﹣5)
,﹣5)
故答案为:(![]() ,﹣5)
,﹣5)
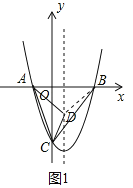
(3)过点E作EG⊥x轴于点G,交直线BC与点F
设E(t,t2﹣t﹣6)(0<t<3),则F(t,2t﹣6)
∴EF=2t﹣6﹣(t2﹣t﹣6)=﹣t2+3t
∴S△BCE=S△BEF+S△CEF=![]() EFBG+
EFBG+![]() EFOG=
EFOG=![]() EF(BG+OG)=
EF(BG+OG)=![]() EFOB=
EFOB=![]() ×3(﹣t2+3t)=﹣
×3(﹣t2+3t)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]()
∴当t=![]() 时,△BCE面积最大
时,△BCE面积最大
∴yE=(![]() )2﹣
)2﹣![]() ﹣6=﹣
﹣6=﹣![]()
∴点E坐标为(![]() ,﹣
,﹣![]() )时,△BCE面积最大,最大值为
)时,△BCE面积最大,最大值为![]() .
.
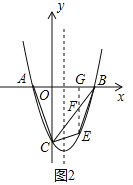
(4)存在点N,使以点A、C、M、N为顶点的四边形是菱形.
∵A(﹣2,0),C(0,﹣6)
∴AC=![]()
①若AC为菱形的边长,如图3,
则MN∥AC且,MN=AC=2![]()
∴N1(﹣2,2![]() ),N2(﹣2,﹣2
),N2(﹣2,﹣2![]() ),N3(2,0)
),N3(2,0)
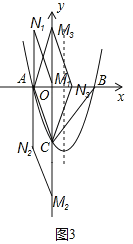
②若AC为菱形的对角线,如图4,则AN4∥CM4,AN4=CN4
设N4(﹣2,n)
∴﹣n=![]()
解得:n=﹣![]()
∴N4(﹣2,﹣![]() )
)
综上所述,点N坐标为(﹣2,2![]() ),(﹣2,﹣2
),(﹣2,﹣2![]() ),(2,0),(﹣2,﹣
),(2,0),(﹣2,﹣![]() ).
).


科目:初中数学 来源: 题型:
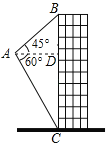
【题目】如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为_____m.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
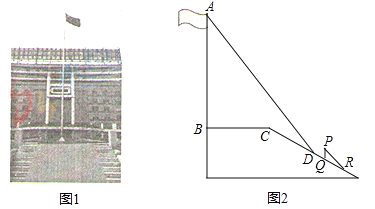
【题目】(2016山东省烟台市)某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
查看答案和解析>>
科目:初中数学 来源: 题型:
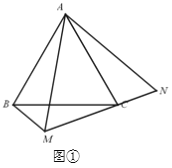
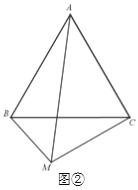
【题目】已知△ABC为等边三角形, M为三角形外任意一点,把△ABM绕着点A按逆时针方向旋转60°到△CAN的位置.
(1)如图①,若∠BMC=120°,BM=2,MC=3.求∠AMB的度数和求AM的长.
(2)如图②,若∠BMC = n°,试写出AM、BM、CM之间的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=5,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=![]() CE时,EP+BP的值为( )
CE时,EP+BP的值为( )
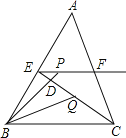
A.10B.8C.6D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
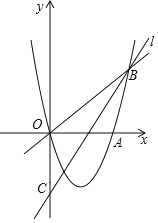
【题目】如图,抛物线y=ax2+bx+c经过O、A(4,0)、B(5,5)三点,直线l交抛物线于点B,交y轴于点C(0,﹣4).点P是抛物线上一个动点.
(1)求抛物线的解析式;
(2)点P关于直线OB的对称点恰好落在直线l上,求点P的坐标;
(3)M是线段OB上的一个动点,过点M作直线MN⊥x轴,交抛物线于点N.当以M、N、B为顶点的三角形与△OBC相似时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD被分割成两个小梯形①②,和一个小正方形③,去掉③后,①和②可剪拼成一个新的梯形,若EF﹣AD=2,BC﹣EF=1,则AB的长是( )
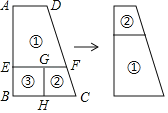
A.6B.3![]() C.9D.3
C.9D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,顺次连接各边中点得正方形A1B1C1D1,又依次连接正方形A1B1C1D1各边中点得正方形A2B2C2D2,以此规律已知作下去,那么正方形A8B8C8D8的周长是 .
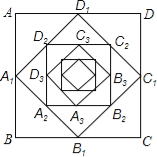
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com