
如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
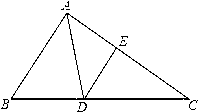
【考点】相似三角形的判定与性质.
【分析】(1)利用已知条件易证AB∥DE,进而证明△DCE∽△BCA;
(2)首先证明AE=DE,设DE=x,所以CE=AC﹣AE=AC﹣DE=4﹣x,利用(1)中相似三角形的对应边成比例即可求出x的值,即DE的长.
【解答】(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DA,
∵∠EAD=∠ADE,
∴∠BAD=∠ADE,
∴AB∥DE,
∴△DCE∽△BCA;
(2)解:∵∠EAD=∠ADE,
∴AE=DE,
设DE=x,
∴CE=AC﹣AE=AC﹣DE=4﹣x,
∵△DCE∽△BCA,
∴DE:AB=CE:AC,
即x:3=(4﹣x):4,
解得:x=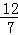 ,
,
∴DE的长是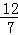 .
.
【点评】本题考查了相似三角形的判定和性质、平行线的判定和性质、等腰三角形的判定和性质,题目的综合性较强,难度不大.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
.如图1,直线y=2x与反比例函数y=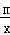 的图象交于点A(3,n),点B是线段OA上的一个动点.
的图象交于点A(3,n),点B是线段OA上的一个动点.
(1)则m=18,OA=3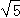 ;
;
(2)将三角板的直角顶点放置在点B处,三角 板的两条直角边分别交x轴、y轴于C、D两点,求
板的两条直角边分别交x轴、y轴于C、D两点,求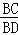 的值;
的值;
(3)如图2,B是线段OA的中点,E在反比例函数的图象上,试探究:在x轴上是否存在点F,使得∠EAB=∠EBF=∠AOF?如果存在,试求出点F的坐标;如果不存在,请说明理由.
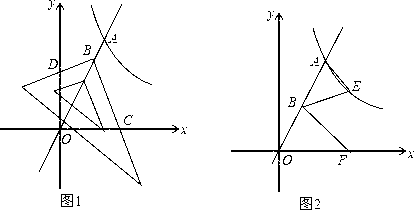
查看答案和解析>>
科目:初中数学 来源: 题型:
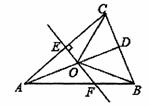
如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等的三角形的对数是 ( )
A.2对 B.3对 C.4对 D.5对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com