【题目】方程x（x+1）=5（x+1）的根是（ ）
A.﹣1
B.5
C.1或5
D.﹣1或5
天天向上一本好卷系列答案科目：初中数学 来源： 题型：
【题目】如图，正方形AOCB在平面直角坐标系xoy中，点O为原点，点B在反比例函数
（x＞0）图象上，△BOC的面积为8．
（1）求反比例函数
的关系
（2）若动点E从A开始沿AB向B以每秒1个单位的速度运动，同时动点F从B开始沿BC向C以每秒2个单位的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动．若运动时间用t表示，△BEF的面积用S表示，求出S关于t的函数关系式？
（3）当运动时间为
秒时，在坐标轴上是否存在点P，使△PEF的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填写下列空格，完成证明．
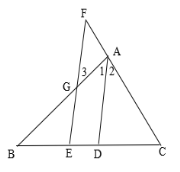
已知：如图，AD是△ABC的角平分线，点E在BC上，点F在CA的延长线上，EF∥AD，EF交AB于点G．
求证：∠3=∠F
证明：因为AD是△ABC的角平分线 （ 已知 ）
所以∠1=∠2 （ ）
因为EF∥AD（已知）
所以∠3=∠ （ ）
∠F=∠ （ ）
所以∠3=∠F（ ）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】动手实验：利用矩形纸片(如图1)剪出一个正六边形纸片；再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形) ，如图2．
(1) 做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少？
(2) 在(1)的条件下，当矩形的长为2a时，要使无盖正六棱柱侧面积最大，正六棱柱的高为多少？并求此时矩形纸片的利用率为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把a2﹣4a多项式分解因式，结果正确的是（ ）
A. a（a﹣4） B. （a+2）（a﹣2） C. a（a+2）（a﹣2） D. （a﹣2）2﹣4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们规定一个物体向右运动为正，向左运动为负.如果该物体向左连续运动两次，每次运动3 米，那么下列算式中，可以表示这两次运动结果的是( )
A. （－3）2 B. （－3）－（－3） C. 2×3 D. 2×（－3）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠AOB＝α，将△DOC按逆时针方向旋转得到△D′OC′（0°＜旋转角＜90°）连接AC′、BD′，AC′与BD′相交于点M．
(1)、当四边形ABCD为矩形时，如图1．求证：△AOC′≌△BOD′．
(2)、当四边形ABCD为平行四边形时，设AC＝kBD，如图2．
①猜想此时△AOC′与△BOD′有何关系，证明你的猜想；
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系，并给予证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，点D是边BC的中点，过点A、D分别作BC与AB的平行线，相交于点E，连结EC、AD．
（1）求证：四边形ADCE是矩形；
（2）当∠BAC=90°时，求证：四边形ADCE是正方形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
