
分析 (1)首先求出m和n的值,进而判断出m和n均小于0,然后进行分式的化简,最后整体代入求值;
(2)根据m和n小于0化简$\sqrt{\frac{{m}^{3}}{n}}$+$\sqrt{\frac{{n}^{3}}{m}}$为$\sqrt{mn}$($\frac{(m+n)^{2}-2mn}{mn}$),然后根据m+n=-3,mn=1整体代值计算.
解答 解:(1)∵m,n是方程x2+3x+1=0的两根,
∴m=$\frac{-3-\sqrt{5}}{2}$,n=$\frac{\sqrt{5}-3}{2}$,
∴m<n<0,
原式=$\frac{25{-m}^{2}-16}{5-m}$•$\frac{2(m-5)}{3-m}$-$\frac{2}{m}$
=$\frac{2{(m}^{2}-9)}{3-m}$-$\frac{2}{m}$
=-6-2m-$\frac{2}{m}$
=$\frac{-2({m}^{2}+3m+1)}{m}$
∵m,n是方程x2+3x+1=0的两根,
∴m2+3m+1=0,
∴原式=0;
(2)∵m<0,n<0,
∴$\sqrt{\frac{{m}^{3}}{n}}$+$\sqrt{\frac{{n}^{3}}{m}}$=-m$\sqrt{\frac{m}{n}}$-n$\sqrt{\frac{n}{m}}$=$\frac{m}{n}\sqrt{mn}$+$\frac{n}{m}\sqrt{mn}$=$\sqrt{mn}$($\frac{(m+n)^{2}-2mn}{mn}$),
∵m+n=-3,mn=1,
∴原式=9-2=7.
点评 本题主要考查了根与系数的关系、分式的化简求值以及代数求值等知识,解答本题的关键是能求出m和n的判断出m和n均小于0,此题难度一般.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2.
小刚用一张半径为12cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为5cm,那么这张扇形纸板的面积是60πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
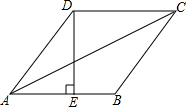 如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.
如图所示,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com