
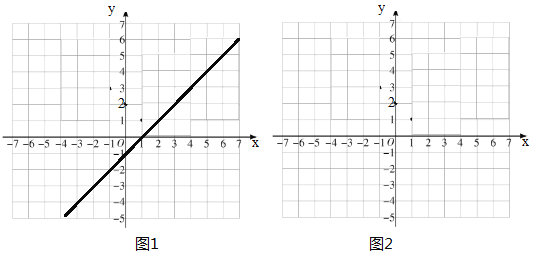
【题目】(1)如图1,结合函数![]() 的图象填空:
的图象填空:![]() 随
随![]() 的增大而___________,当
的增大而___________,当![]() 时,该函数的最大值为_________,最小值为_________.
时,该函数的最大值为_________,最小值为_________.
(2)根据学习函数的经验来探究函数![]() 的最小值.
的最小值.
①若点![]() 和点
和点![]() 是该函数图象上的两点,则
是该函数图象上的两点,则![]() _________;
_________;
②在平面直角坐标系中描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;
③由图象可知,函数![]() 的最小值为___________.
的最小值为___________.
(3)请结合![]() 的取值范围判断方程
的取值范围判断方程![]() 的解的个数.(直接写出结果)
的解的个数.(直接写出结果)
【答案】(1)增大,2,![]() ;(2)①2;②详见解析;③1;(3)当
;(2)①2;②详见解析;③1;(3)当![]() 时,原方程无解,当
时,原方程无解,当![]() 时,原方程有1个解,当
时,原方程有1个解,当![]() 时,原方程有两个不相等的解(或有两个解).
时,原方程有两个不相等的解(或有两个解).
【解析】
(1)根据一次函数的性质及函数图象上点的坐标特征即可得到答案;
(2)①去掉绝对值符号得到函数的解析式为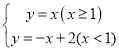 ,把点
,把点![]() 和点
和点![]() 的坐标分别代入计算即可求得答案;
的坐标分别代入计算即可求得答案;
②通过列表、描点、连线即可画出该函数的图象;
③观察函数的图象即可获得答案;
(3)当![]() 、
、![]() 、
、![]() 时,分别讨论方程
时,分别讨论方程![]() 的解的个数即可.
的解的个数即可.
(1)观察函数![]() 的图象,
的图象,![]() 随
随![]() 的增大而增大,
的增大而增大,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴当![]() 时,该函数的最大值为2,最小值为-2,
时,该函数的最大值为2,最小值为-2,
故答案为:增大,2,![]() ;
;
(2)①函数![]() 的解析式为
的解析式为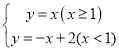 ,
,
∵点![]() 和点
和点![]() 纵坐标相等,
纵坐标相等,
∴点![]() 和点
和点![]() 分别在两个函数的图象上,
分别在两个函数的图象上,
不妨设点![]() 在
在![]() 的图象上,则点
的图象上,则点![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,
,![]() ,
,
即![]() ,
,
解得:![]() ,
,
故答案为:![]() ;
;
② 列表得:
|
| -2 | -1 | 0 | 1 | 2 | 3 | 4 |
|
|
| 4 | 3 | 2 | 1 | 2 | 3 | 4 |
|
描点、连线,如图所示:
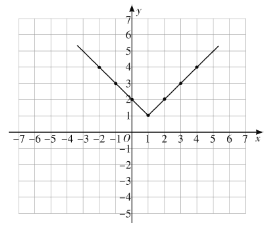
③观察函数的图象可知:当![]() 时,函数取得最小值为: 1,
时,函数取得最小值为: 1,
故答案为:1;
(3)观察函数的图象,
当![]() 时,原方程无解,
时,原方程无解,
当![]() 时,原方程有1个解,
时,原方程有1个解,
当![]() 时,原方程有两个不相等的解.
时,原方程有两个不相等的解.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 移动,同时点
移动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线移动,点
的延长线移动,点![]() ,
,![]() 移动的速度相同,
移动的速度相同,![]() 与
与![]() 相交于点
相交于点![]() .
.
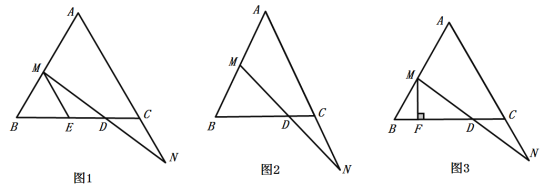
(1)如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() ,当点
,当点![]() 移动到
移动到![]() 的中点时,求
的中点时,求![]() 的长度;
的长度;
(3)如图3,过点![]() 作
作![]() 于点
于点![]() .在点
.在点![]() 从点
从点![]() 向点
向点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)移动的过程中,线段
重合)移动的过程中,线段![]() 与
与![]() 的长度是否保持不变若保持不变,请求出
的长度是否保持不变若保持不变,请求出![]() 与
与![]() 的长度和;若改变,请说明理由.
的长度和;若改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.
试问:(1)规定日期是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校创客小组进行机器人跑步大赛,机器人小![]() 和小
和小![]() 从同一地点同时出发,小
从同一地点同时出发,小![]() 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有_________ (填序号).
在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有_________ (填序号).
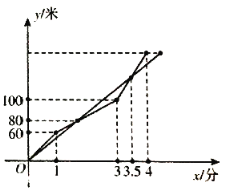
①两个机器人第一次相遇时间是在第2分钟;
②小![]() 每分钟跑50米;
每分钟跑50米;
③赛程总长200米;
④小![]() 到达终点的时候小
到达终点的时候小![]() 距离终点还有20米.
距离终点还有20米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交于
轴正半轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,且
,且![]() ,则下列结论:
,则下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④关于
;④关于![]() 的方程
的方程![]() 有一个根为
有一个根为![]() ,其中正确的结论个数有( )
,其中正确的结论个数有( )
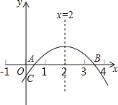
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,与函数y=![]() x+b的图象交于点C(﹣2,m).
x+b的图象交于点C(﹣2,m).
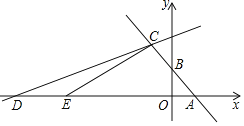
(1)求m和b的值;
(2)函数y=![]() x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
①当△ACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使△ACE为直角三角形?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com