
【题目】某学校创客小组进行机器人跑步大赛,机器人小![]() 和小
和小![]() 从同一地点同时出发,小
从同一地点同时出发,小![]() 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有_________ (填序号).
在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有_________ (填序号).
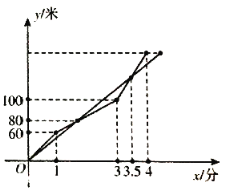
①两个机器人第一次相遇时间是在第2分钟;
②小![]() 每分钟跑50米;
每分钟跑50米;
③赛程总长200米;
④小![]() 到达终点的时候小
到达终点的时候小![]() 距离终点还有20米.
距离终点还有20米.
【答案】①④
【解析】
利用待定系数法求出线段AB的解析式,然后当y=80时代入解析式就可以求出两人第一次相遇的时间,可以判断①正确;此时小![]() 2分钟跑了80米,求得小
2分钟跑了80米,求得小![]() 的速度判断②错误;运用待定系数法求出OD的解析式,求得点F的坐标,再用待定系数法求出BC的解析式,当
的速度判断②错误;运用待定系数法求出OD的解析式,求得点F的坐标,再用待定系数法求出BC的解析式,当![]() 时代入解析式求出全程判断③错误;当
时代入解析式求出全程判断③错误;当![]() 时求得此时小
时求得此时小![]() 走的路程,判断④正确.
走的路程,判断④正确.
①设线段AB的解析式为![]() ,由图象得:
,由图象得:
A (1,60),B (3,100),
∴ ,
,
解得: ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
解得:![]() ,此时E点的坐标为(2,80),
,此时E点的坐标为(2,80),
故比赛2分钟时两机器人第一次相遇,故①正确;
此时小![]() 2分钟跑80米,小
2分钟跑80米,小![]() 的速度为:
的速度为:![]() 米/分,
米/分,
即小![]() 每分钟跑40米,故②错误;
每分钟跑40米,故②错误;
设线段OD的解析式为![]() ,
,
∵线段OD经过点E(2,80),
∴![]() ,
,
解得:![]() ,
,
∴线段OD的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴点F的坐标为(3.5,140),
设线段BC的解析式为![]() ,
,
∵BC经过:B (3,100),F (3.5,140),
 ,
,
解得: ,
,
则![]() ,
,
当![]() 时,
时,![]() ,
,
∴点C的坐标为(4,180),
∴总赛程长为180米,故③错误;
当小![]() 到达终点的时小
到达终点的时小![]() 也走了4分钟,
也走了4分钟,
即当![]() 时,
时,![]() ,
,
∴小![]() 距离终点还有
距离终点还有![]() 米,故④正确;
米,故④正确;



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商店经销一种成本为每千克![]() 元的水产品,据市场分析,若按每千克
元的水产品,据市场分析,若按每千克![]() 元销售,一个月能售出
元销售,一个月能售出![]() ,销售单价每涨(或跌)
,销售单价每涨(或跌)![]() 元,月销售量就减少(或增加)
元,月销售量就减少(或增加)![]() ,解答以下问题:
,解答以下问题:
(1)当销售单价定位每千克![]() 元时,计算月销售量和月销售利润;
元时,计算月销售量和月销售利润;
(2)商店想在月销售成本不超过![]() 元的情况下,使得月销售利润达到
元的情况下,使得月销售利润达到![]() 元,销售单价应为多少?
元,销售单价应为多少?
(3)商店要使得月销售利润达到最大,销售单价应为多少?此时利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
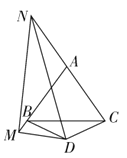
【题目】如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探BM,MN,CN之间的数量关系,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.
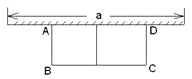
(1)求S与x的函数关系式;
(2)如果要围成面积为45m2的花圃,AB的长是多少米?
(3)能围成面积比45 m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
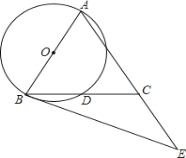
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,点E在AC的延长线上,且∠CBE=![]() ∠BAC.
∠BAC.
(1)求证:BE是⊙O的切线;
(2)若∠ABC=65°,AB=6,求劣弧AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,结合函数![]() 的图象填空:
的图象填空:![]() 随
随![]() 的增大而___________,当
的增大而___________,当![]() 时,该函数的最大值为_________,最小值为_________.
时,该函数的最大值为_________,最小值为_________.
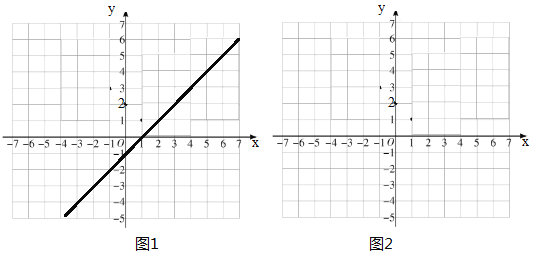
(2)根据学习函数的经验来探究函数![]() 的最小值.
的最小值.
①若点![]() 和点
和点![]() 是该函数图象上的两点,则
是该函数图象上的两点,则![]() _________;
_________;
②在平面直角坐标系中描出以上表中各对对应值为坐标的点,并根据描出的点,画出该函数的图象;
③由图象可知,函数![]() 的最小值为___________.
的最小值为___________.
(3)请结合![]() 的取值范围判断方程
的取值范围判断方程![]() 的解的个数.(直接写出结果)
的解的个数.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
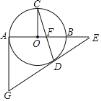
【题目】如图,![]() 为
为![]() 直径,
直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,弦
,弦![]() 与
与![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,使
,使![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .过点
.过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求弧
,求弧![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖南师大附中组织集团校内七、八、九年级学生参加“12KM”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
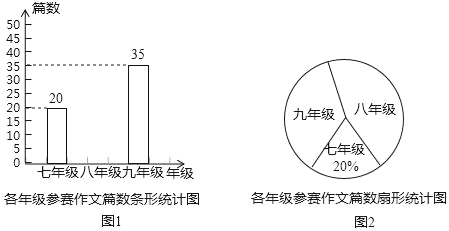
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度.八年级参赛作文篇数对应的百分比是 .
(2)请补全条形统计图.
(3)经过评审,全集团校内有4篇作文荣获特等奖,其中一篇来自九年级,学校准备从特等奖作文中任选两篇刊登在校报上,请利用画树状图或列表的方法求出九年级特等奖作文被选登在校报上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com