
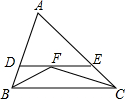
 如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论:①△BDF、△CEF都是等腰三角形;②DE=DB+CE;③AD+DE+AE=AB+AC;④BF=CF.正确的有①②③.
如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,那么下列结论:①△BDF、△CEF都是等腰三角形;②DE=DB+CE;③AD+DE+AE=AB+AC;④BF=CF.正确的有①②③. 分析 根据平分线的性质、平行线的性质,借助于等量代换可求出∠DBF=∠DFB,即△BDF是等腰三角形,同理△CEF都是等腰三角形;进而利用等腰三角形的性质解答即可.
解答 解:①∵BF是∠ABC的角平分线,
∴∠ABF=∠CBF,
又∵DE∥BC,
∴∠CBF=∠DFB,
∴DB=DF即△BDF是等腰三角形,
同理∠ECF=∠EFC,
∴EF=EC,
∴△BDF,△CEF都是等腰三角形;
∵∠B、∠C的角平分线交于点F,
∴∠DBF=∠CBF(设为α),∠ECF=∠BCF(设为β);
∵DE∥BC,
∴∠DFB=∠CBF=α,∠EFC=∠BCF=β;
∴∠DBF=∠DFB,∠EFC=∠ECF,
∴DB=DF,EF=EC;
∴DE=DB+CE,AD+DE+AE=AB+AC,②③正确;
AB和AC不一定相等,∴BF和CF不一定相等.故④错误
故答案为:①②③
点评 该题主要考查了等腰三角形的判定、平行线的性质等几何知识点的应用问题;灵活运用等腰三角形的判定、平行线的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
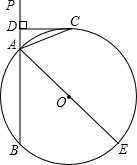 如图所示,已知直线PA交☉O于A、B两点,AE是☉O的直径,C为☉O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂直为D.
如图所示,已知直线PA交☉O于A、B两点,AE是☉O的直径,C为☉O上一点,且AC平分∠PAE,过点C作CD⊥PA,垂直为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
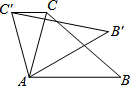 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com